More Information
Submitted: July 03, 2025 | Approved: July 19, 2025 | Published: July 21, 2025
How to cite this article: Aime AL, Musabe R, Gatera O, Hitimana E. Optimizing LoRaWAN Performance through Learning Automata-based Channel Selection. J Artif Intell Res Innov. 2025; 1(1): 006-012. Available from:
https://dx.doi.org/10.29328/journal.jairi.1001002
DOI: 10.29328/journal.jairi.1001002
Copyright license: © 2025 Aime AL, et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Keywords: Channel selection; Pursuit; Learning automata; Estimator based – LA; LoRaWAN; HCPA; HDPA
Optimizing LoRaWAN Performance through Learning Automata-based Channel Selection
Atadet Luka Aime1*, Richard Musabe1, Omar Gatera2 and Eric Hitimana1
1School of Information and Communication Technology (SoICT), College of Science and Technology, University of Rwanda, Rwanda
2African Centre of Excellence in Internet of Things, College of Science and Technology, University of Rwanda, Rwanda
*Address for Correspondence: Atadet Luka Aime, School of Information and Communication Technology (SoICT), College of Science and Technology, University of Rwanda, Rwanda, Email: [email protected]
The rising demand for long-range, low-power wireless communication in applications such as monitoring, smart metering, and wide-area sensor networks has emphasized the critical need for efficient spectrum utilization in LoRaWAN (Long Range Wide Area. Network). In response to this challenge, this paper proposes a novel channel selection framework based on Hierarchical Discrete Pursuit Learning Automata (HDPA), aimed at enhancing the adaptability and reliability of LoRaWAN operations in dynamic and interference-prone environments. The HDPA framework capitalizes on the adaptive decision-making capabilities of Learning Automata (LA) to monitor and predict channel conditions in real time, enabling intelligent and sequential channel selection that maximizes transmission performance while reducing packet loss and co-channel interference. By integrating a hierarchical structure and discrete pursuit learning strategy, the proposed model achieves improved learning speed and accuracy in identifying optimal transmission channels from diverse frequency options. The methodology includes a detailed theoretical formulation of the HDPA algorithm and extensive simulations to evaluate its performance. Results demonstrate that HDPA outperforms Hierarchical Continuous Pursuit Automata (HCPA), particularly in convergence speed and selection accuracy.
The proliferation of the Internet of Things (IoT) and the associated demand for ubiquitous, low-power, and long-range wireless communication has propelled the development and adoption of Long Range Wide Area Network (LoRaWAN) systems [1]. LoRaWAN offers a compelling framework for IoT.
Applications due to its ability to provide wide-area coverage with minimal energy consumption [2]. However, as deployments expand, especially in urban and industrial environments with increasing device densities, maintaining high network performance becomes a significant challenge [3]. The core difficulty lies in effective radio channel selection amid dynamic, congested, and interference-prone environments.
Despite the widespread deployment of LoRaWAN in large-scale IoT systems, a critical limitation like the lack of intelligent, adaptive, and context-aware channel selection mechanisms.
Furthermore, the traditional channel access scheme fails to incorporate feedback mechanisms that allow devices to learn past transmissions or adapt their strategies based on observed outcomes. This is especially problematic in stochastic environments, where channel quality fluctuates due to external interference, environmental changes. Without the ability to dynamically adjust to these variations, LoRaWAN networks remain vulnerable to congestion.
There is a pressing need for a lightweight, decentralized, and intelligent channel selection solution that can adapt its decisions in real time. Such a solution should be able to maximize successful transmission.
To address this, our research introduces a Learning Automata (LA)-based solution, specially the Hierarchical Pursuit Learning Automata (HDPA), as an optimal channel selection mechanism for LoRaWAN, Learning Automata, a class of Reinforcement learning algorithms, operate by interacting with a stochastic environment to identify the best actions through trial-error processes based on reward and penalties [5]. The HDPA model extends traditional LA by employing a hierarchical structure that allows for faster and more accurate convergence to the optimal channel, especially in multi-step, dynamic environments like LoRaWAN.
This study proposed the integration of HDPA into LoRaWAN as a predictive, self-adapting algorithm capable of identifying the most reliable communication channels based on ongoing transmission success rates. Unlike static models, HDPA continually updates its selection probabilities using environmental feedback, optimizing network performance through a structured decision-making framework. The learning mechanism evaluates multiple channels in parallel, dynamically adapting to network behavior and reducing the impact of interference, collisions, and congestion [6].
The objectives of this research are multifaceted: to critically review existing channel selection techniques in LoRaWAN and their limitations; to design and implement the HDPA model for LoRaWAN environments; and to evaluate the model’s performance against existing solutions such as Hierarchical Continuous Pursuit Automata (HCPA) through rigorous simulations [7]. We hypothesize that HDPA will demonstrate superior performance in terms of throughput, convergence speed, and decision-making accuracy.
The proposed methodology combines theoretical modeling, algorithmic design, and simulation-based validation using MATLAB. The simulations are configured with realistic network scenarios, channel characteristics, and iterative experiments to assess metrics like accuracy, standard deviation, and convergence time.
Preliminary results affirm that HDPA significantly outperforms HCPA, especially under high-density and variable channel conditions. With a mean convergence iteration of approximately 6279.64 and an accuracy of 98.78%, HDPA proves to be a highly effective algorithm for channel classification and selection in LoRaWAN.
The main aim of this research is to design and evaluate the Hierarchical Discrete Pursuit Learning Automata (HDPA) as an adaptive channel selection mechanism in the LoRaWAN environment. The study explores how HDPA can learn from network feedback to enhance throughput, reduce interference, and outperform existing methods.
The remainder of this paper is organized as follows. Section 2 provides a detailed summary of the related work. Section 3 describes and analyzes the system model along with the channel selection problems. In Section 4, we introduce the Learning automata-based LoRaWAN channel access scheme. Section 5 presents extensive simulation results that demonstrate the advantages of using HDPA for channel selection. Finally, Section 6 concludes the paper.
Several studies have investigated the optimization of LoRaWAN-based IoT networks using machine learning and analytical approaches. In [8], the authors investigated SF prediction using supervised ML algorithms in a mobile LoRaWAN environment. They evaluated various classifiers, including k-Nearest Neighbors, Decision Trees, Random Forests, and Multinomial Logistic Regression using manually selected features such as RSSI and SNR, antenna height, distance to the gateway, and frequency. The study identified RSSI and SNR as the most significant predictors, achieving around 65% accuracy. However, the model was limited by manual feature selection and a constrained urban dataset. In the context of large-scale smart city deployments [9] employed ML models were employed to predict Estimated Signal Power (ESP) using data collected from over 30,000 smart water meters across Cyprus. Decision Trees and XGBoost classifiers were used to forecast ESP based on environmental and topographical features, to improve network planning and deployment efficiency. Although the models showed high predictive performance, the focus on ESP alone limits broader insights into other critical metrics like packet delivery ratio and throughput.
Addressing coexistence challenges in Low-power Wide-area Networks (LPWANs), [10] proposed an analytical interference model between LoRaWAN and Sigfox networks. The model accounted for parameters such as duty cycle and node density and was validated using SEAMCAT simulations. The concept of “protection distance” was introduced to minimize mutual interference. Despite its theoretical contributions, the model assumed uniform node distribution and ignored dynamic network characteristics such as adaptive SF.
To improve transmission efficiency and data rates, [11] developed a resource allocation algorithm (LRA) for LoRa devices equipped with dual transceivers. The algorithm leveraged the quasi-orthogonality of different SFs to concurrently transmit data, effectively increasing the channel capacity. Evaluations showed significant improvements in transmission time and bit rate, particularly for large data transfers like image transmissions.
Reinforcement Learning has also been explored for decentralized channel selection in dense LoRaWAN environments [12]. Implemented a lightweight Multi-armed Bandit (MAB) algorithm based on Tug-of-War (ToW) dynamics on actual LoRa hardware. Their approach demonstrated superior convergence and channel allocation performance compared to traditional RL strategies like UBC1+Tuned and ε-greedy. However, the evaluation was limited to a small-scale indoor setup with restricted channel diversity. A subsequent study by the same authors [13] tested the MAB-based strategy in urban outdoors environments using Lazurite 920J devices. This follow–up algorithm’s compatibility with coexisting LPWANs like Sigfox. In more complex cognitive radio-based IIoT applications, [14] introduced a dual Q- learning framework for proactive spectrum handoff. By jointly estimating channel availability and RSSI trends, the algorithm minimized latency and improved throughput in dynamic wireless environments. At the MAC layer, slotted Aloha has been proposed as a potential enhancement over pure Aloha in LoRaWAN. [15] used simulations to evaluate the performance of slotted Aloha under different traffic conditions, reporting up to 67% improvement in reducing collisions. Another work presented a Markov-based model to determine the optimal retransmission probability, balancing throughput and delay.
In [16]. The authors develop a comprehensive mathematical model to evaluate the throughput capacity of a LoRaWAN communication channel. The model accounts for key parameters, including Spreading Factor (SF), duty cycle, payload size, and message structure, providing quantitative insights into how these variables impact performance. The study further explores throughput under different regional duty cycle regulations (0.1%, 1%, and 10%), providing valuable guidance for regulatory compliance and deployment planning. It analyzes the trade-offs between message repetitions and range, showing that a reduction in repetitions with higher SF can lead to a 28% increase in throughput.
To address collision management in dense networks, [17] introduces CANL, an open-loop collision avoidance protocol that leverages neighbor listening instead of relying on the unreliable Channel Activity Detection (CAD) mechanism. CANL significantly enhances the Packet Delivery Ratio (PDR) and energy efficiency in dense deployments. The authors also propose CANL RTS, a variant that overcomes hardware limitations by employing a short request-to-send (RTS) frame. Extensive simulation results using an enhanced LoRaSim tool demonstrate CANL’s superiority over traditional ALOHA and CAD+Backoff schemes.
This section outlines the research methodology adopted for the study. A scientific approach forms the foundation of the work, with a strong emphasis on quantitative methods to support experimental analysis. The chosen methods ensure a systematic and objective investigation of the research objectives (Figure 1).
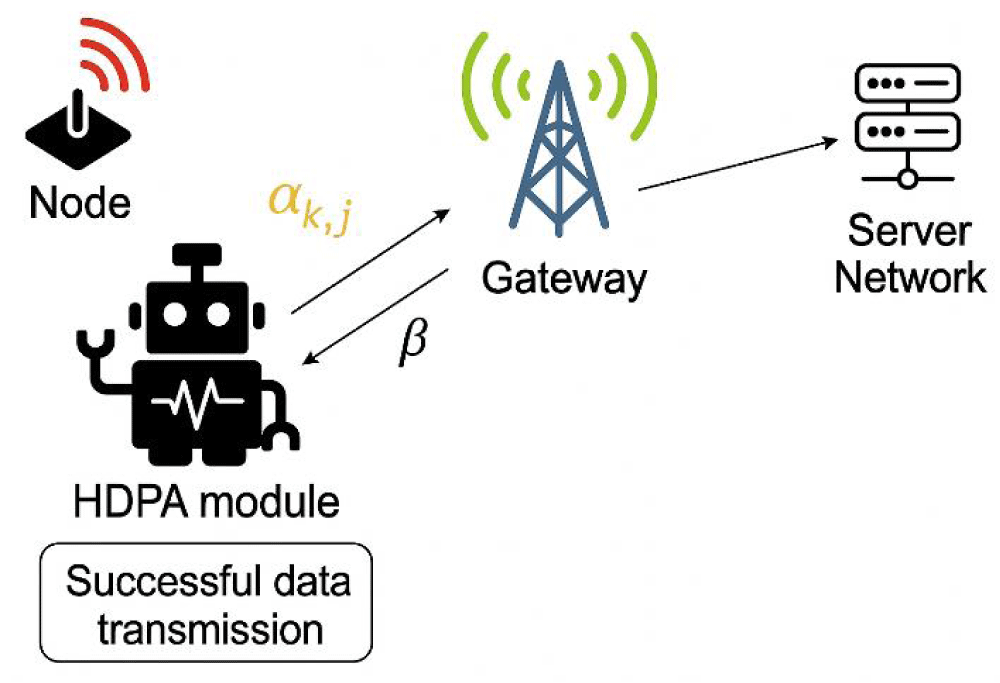
Figure 1: Proposed LoRa Network Model This model consists of several key components that work together to optimize data transmission through learning and feedback mechanisms.
A. System model
The node is an end device equipped with a radio transmitter that sends data packets. The decision maker represented by the robot implements the Hierarchical Discrete Pursuit Learning Automata (HDPA) algorithms. Its role is to select the optimal radio channel for data transmission based on past transmission success rate feedback from the gateway. The decision maker updates the probability distribution of channel selection using the number of times it received a reward over the number of times it was selected.
The feedback loop represents the action taken by the decision maker regarding which channel to use for the next data transmission. Beta represents the feedback received from the gateway. If the transmission is successful, the decision maker receives positive feedback reinforcing the chosen channel. If unsuccessful, the decision maker receives negative feedback, decreasing the likelihood of selecting that channel again.
B. Proposed algorithm flowchart
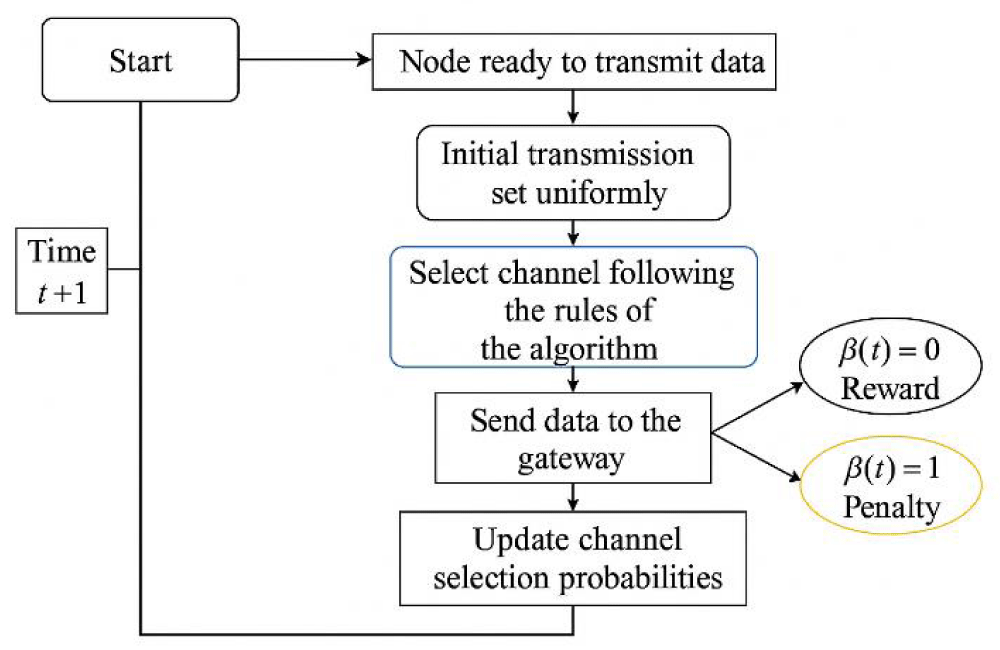
In terms of process flow, the node transmits data to the gateway using a channel selected by the decision-maker. The gateway provides feedback on the transmission’s success. Positive feedback increases the probability of selecting a successful channel in the future, while negative feedback decreases the probability of encouraging the decision maker to explore other channels. The decision maker then continuously updates its channel selection probabilities based on the feedback, adapting to the dynamic network environment to optimize data transmission reliability (Figure 2).
Figure 2: Simulation flow chart.
C. Mathematical development
Algorithm t = 0
Loop
1. Depths from 0 to K-1:
𝒜 [0,1] selects a channel by randomly sampling as per its channel probability vector [𝑝{1,1}(𝑡), 𝑝{1,2}(𝑡)]. We denote 𝑗1(𝑡) as the chosen channel at depth 0 with 𝑗11(𝑡)𝜖 {1,2}.
𝒜 {1, 𝑗1(𝑡)}, 𝑗1(𝑡)} chooses a channel and activates the next LA at depth «2».
The process continues until K-1, which is the level that chooses the channel.
2. Depth K:
The index of the channel chosen at depth K is denoted
(𝑡) 𝜖 {1, . . . 2K}.
Update the estimated chance of reward based on the response received from the environment at leaf depth K:
𝑢 {𝐾, (𝑡)} (𝑡 + 1) = 𝑢 {𝐾, 𝐽𝑘(𝑡)}(𝑡) + (1 − 𝛽(𝑡))
𝑣 {𝐾, (𝑡)} (𝑡 + 1) = 𝑣 {𝐾, 𝐽𝑘(𝑡)} (𝑡) + 1
For the other channel at the leaf, where 𝑗 𝜖 {1, . . ., 2𝐾} and
3. Define the reward estimate recursively for all subsequent channels along the path to the root, 𝑘 𝜖 {0,..., 𝐾 − 1}, where 𝒜 at any one level inherits the feedback from the 𝒜 at the level below:
Update the channel probability vectors along the path to the leaf with the current maximum reward estimate:
Each 𝒜 𝑗 𝜖 {1, . . ., 2𝑘} at depth k where 𝑘 𝜖 {0, . . ., 𝐾 − 1} has two channels 𝛼 {𝑘 + 1,2𝑗 − 1} and 𝛼 {𝑘 + 1,2𝑗}.
4. We denote the larger element between and
and the lower reward estimate as
Update P{k+1,𝑗𝑘ℎ+1(𝑡)} and/or using the estimate for all
𝑘 𝜖 {0, . . ., 𝐾 − 1} as: If 𝛽(𝑡) = 0 Then
P{k+1 ,𝑗𝑘ℎ+1(𝑡)}(t + 1) = min (P{k+1 ,𝑗𝑘ℎ+1(𝑡)}(t) + Δ, 1),
𝑘+1
Else
β(𝑡) = 1 Then
P{k+1 ,𝑗𝑘ℎ+1(𝑡)}(t + 1) = max (P{k+1 ,𝑗𝑘ℎ+1(𝑡)}(t) + Δ, 0),
𝑘+1
,
End if
5. For each Learning Automata, if either of its channel selection probabilities surpasses a threshold T, with T being a positive number close to unity, the channel probability will stop updating, meaning the convergence is achieved.
6. t = t + 1
End Loop
D. Software environment
MATLAB is chosen for its robust capabilities and extensive support for simulations involving complex algorithms and network models.
E. System simulation
This process combines theoretical modeling with practical experiments to validate the hypothesis that HDPA can enhance the efficiency and reliability of channel selection in LoRaWAN networks.
The simulation setup begins with the configuration of the node to transmit data packets. This node represents an end device in the LoRaWAN network, equipped with a radio transmitter. The simulation adheres to the channel access mechanism defined in the LoRa Alliance [18]. The node interacts with the gateway, responsible for receiving the transmitted data. The gateway acts as an intermediary, forwarding the data to a server network for processing and storage.
At the heart of the simulation is the decision maker, which implements the HDPA algorithm. The decision maker selects the optimal radio channel for data transmission based on the feedback from the previous transmissions. This feedback involves the gateway providing success or failure notifications for each transmission, which the decision maker uses to update its channel selection probabilities.
The simulation is conducted in a MATLAB software environment, chosen for its robust capabilities in handling complex algorithms, providing a platform for running extensive simulations to assess performance under various conditions. The simulation parameters include the node, the channel available the successful data transmission.
Throughout the simulation, key performance metrics are monitored. Including accuracy, the overall network throughput, Std, and speed. By analyzing these metrics, the effectiveness of the HDPA can be evaluated.
F. Simulation variable
| Variable | Symbol | Description |
| Number of channels | 𝑁 | Total number of available channels in the network. |
| Initial channel probability | 𝑃(0) | Initial probability vector for channel selection, 𝑃(0) = [𝑝1, 𝑝2, … , 𝑝𝑁] |
| Reward | 𝑅 | Reward metric for successful transmission on a channel, such as PDR, SNR. |
| Learning Rate | 𝛿 | Step size for probability updates. |
| Hierarchical levels | 𝐿 | Number of levels in the HDPA hierarchy. |
| Convergence threshold | 𝐵 | The threshold for convergence, indicating when the algorithm has likely found the optimal channel. |
| Maximum iteration | 𝑇 | Maximum number of iterations for the simulation. |
| Action selection probability | 𝑃𝑖 | Probability of selecting channels at iteration. |
| Reward estimate | 𝑑𝑖 | Estimate of the reward for channel i. |
| Channel State | 𝑆 | The state of each channel is either idle or busy. |
| Network topology | / | Random |
| Number of nodes | / | 2 end devices |
This section has detailed the methodological framework used to assess the HDPA algorithm for channel selection in LoRaWAN. By combining theoretical modeling with simulation-based validation and by outlining the system model and algorithmic structure, the study establishes a solid foundation for evaluating HDPA’s performance. The next section presents and analyzes the results obtained through this methodology.
This section presents the outcomes of employing Learning Automata into LoRaWAN, highlighting the critical importance of efficient channel selection for network performance, aiming to test the effectiveness of HDPA. We present a comprehensive result from the simulation that was conducted and discuss the implications of these findings. This analysis not only highlights the strengths of HDPA but also compares it with HCPA.
(1)
Where Xi is the number of iterations in the i-th trial. n: the total number of iterations.
(2)
Standard deviation = √Variance (3)
The performance of HDPA is demonstrated here using the formula above and carrying out the simulation results to ensure the effectiveness of our simulations; we set our number of iterations to be 9000 and 10,000, using 200 experiments, expecting that the HDPA with the highest successful transmission probability would converge faster and select the best channel (Table 1).
| Table 1: List of successful data transmission probabilities for 8 channels. |
|||||||
| Α1 | Α2 | Α3 | Α4 | Α5 | Α6 | Α7 | Α8 |
| 0.199 | 0.282 | 0.394 | 0.499 | 0.681 | 0.698 | 0.971 | 0.999 |
The simulation was done for the environment with 8 channels on a benchmark successful transmission probabilities list in Figure 3, showing the probability of the actions with successful transmission, meaning the action with 𝛽 = 0, which is a reward from the environment.
Figure 3: Reward probabilities for 8 channels.
Our simulation shows that the HDPA with a small Learning parameter can converge to the optimal channel with highly successful data transmission, and a higher learning parameter leads to fast convergence to the optimal channel; however, when we set the Learning parameter higher than 0.00087, the algorithm did not converge to the best channel with a successful transmission probability. Therefore, to find the optimal channel with a higher speed of convergence, we decreased the Learning parameter step by step until we achieved 98.78% accuracy. From this value, the algorithm converged to the optimal channel, but took all the iterations that were set. The Mean value to converge to the optimal channel for the 200 experiments with the convergence criterion of 0.99 was 6,279.64, confirming that the HDPA achieved a 0.99 probability of choosing one of the channels with a std of 131.36% on the benchmark probabilities (Table 2).
| Table 2: Results of our simulations for 8 channels. | |
| Parameter | HDPA |
| Mean | 6,279.64 |
| Std | 131.36 |
| Accuracy | 98.78% |
| Learning parameter | 8.7𝑒−4 |
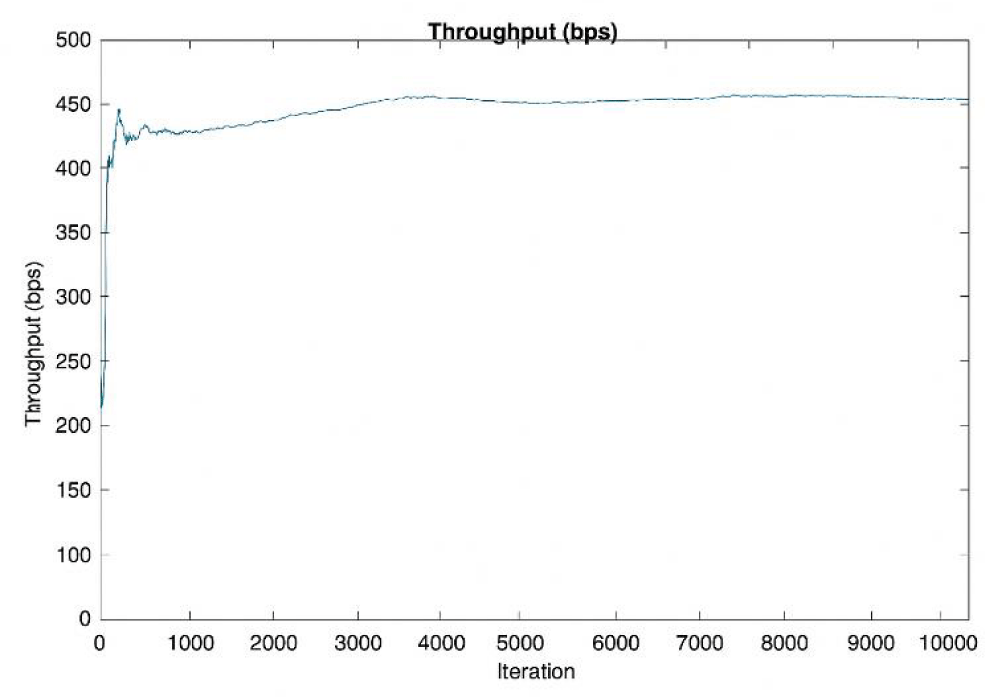
The throughput curve presented in Figure 4 demonstrates the learning behavior of the HDPA algorithm over successive iterations. Initially, the throughput increases sharply, indicating that the algorithm is rapidly acquiring knowledge about the environment and selecting efficient channels. The early phase reflects the exploratory strength of HDPA in adapting to dynamic conditions. As iterations progress, the throughput gradually levels off and stabilizes around 450 bps, signifying convergence to a set of optimal channels. This steady-state performance suggests that HDPA has effectively learned the optimal channel strategy, resulting in sustained high throughput. The graph validates the effectiveness of the proposed approach in optimizing network performance through fast adaptation and robust learning in a fluctuating communication environment.
Figure 4: Throughput.
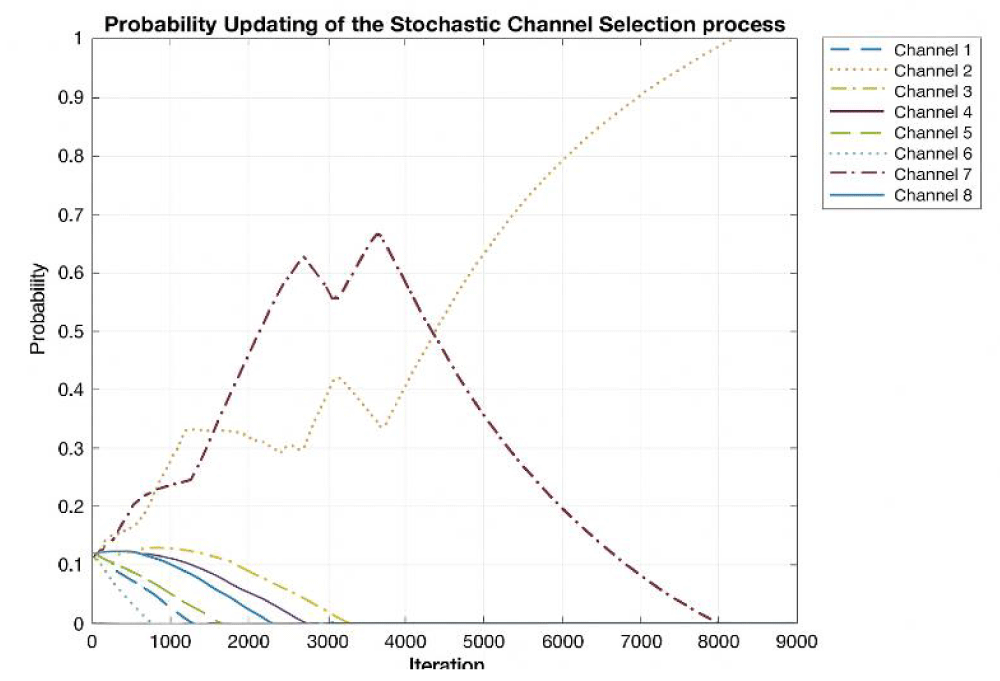
Figure 5 illustrates the process of selecting the most optimal channel from a set of eight available channels. Initially, all channels are explored for communication, with one channel demonstrating a consistently higher probability of successful message transmission, while others perform with comparatively lower success rates. At the beginning of the simulation, there is no prior knowledge regarding which channel is optimal. The Learning Automata mechanism enables the system to gradually converge toward the most effective channel, thereby maximizing throughput. Over time, channels 2 and 7 are identified by the HDPA as the best and second-best channels, respectively. Around iteration 3000, channel 7 temporarily outperforms channel 2. However, due to the stochastic nature of the learning and decision-making process, channel 2 is ultimately selected as the optimal channel, highlighting the HDPA’s capability to balance exploration and exploitation, ensuring adaptability while optimizing long-term performance (Figure 6) (Table 3).
Figure 5: Channel selection updating probability for successful transmission.
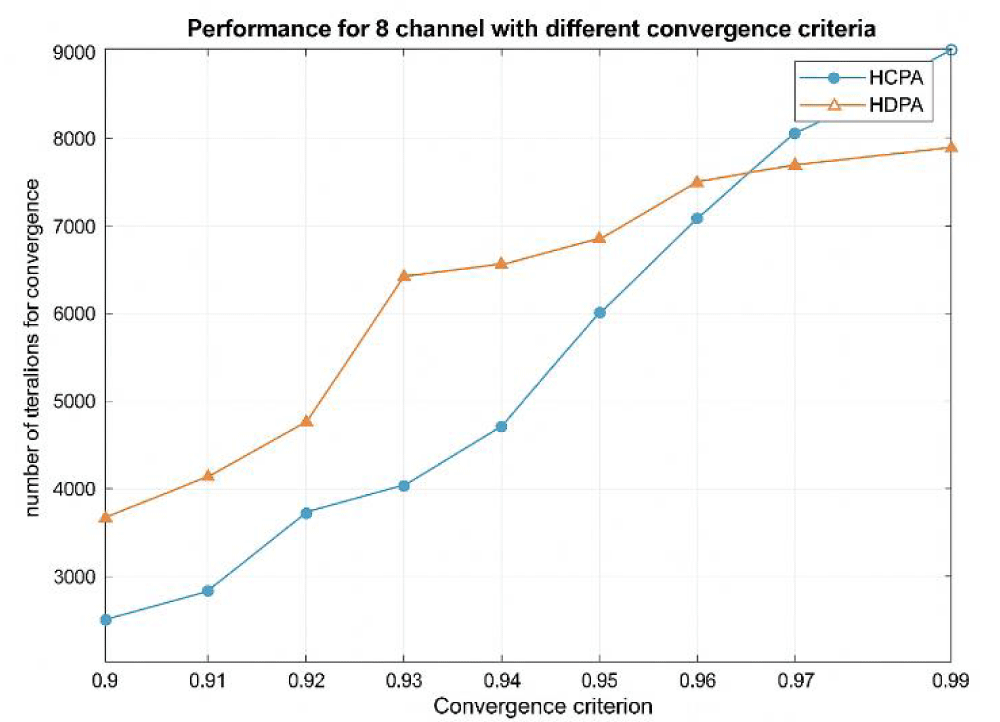
Figure 6: Number of iterations for convergence for 200 experiments.
| Table 3: Comparison between HDPA and HCPA. | ||
| Parameters | HDPA | HCPA |
| Mean | 6,279.64 | 6,778.34 |
| STD | 131.36 | 117.12 |
| Accuracy | 98.78% | 93.89% |
| Learning parameter | 8.7e−4 | 6.9e−4 |
The comparative analysis between HDPA and HCPA, as illustrated in the graph and table, reveals key performance differences. When the convergence criterion was set to 0.9, HCPA outperformed HDPA by converging in approximately 3,500 iterations, compared to over 4,500 for HDPA across 200 experiments. However, as the convergence threshold increased toward 0.99, our target for successful data transmission, HDPA, began to outperform HCPA. For instance, at a convergence level of 0.97, HDPA converged in around 8,000 iterations, while HCPA required about 9,000.
The optimal learning rates identified were 0.00087 for HDPA and 0.00069 for HCPA. In terms of mean iterations to converge, HDPA averaged 6,279.64 with a higher standard deviation, indicating greater variability, whereas HCPA averaged 6,778.34 with a lower standard deviation of 117.12. Importantly, HDPA achieved higher accuracy, close to 99%, making it more effective for precise channel selection in LoRaWAN compared to HCPA.
A. Conclusion
This study has evaluated the performance of the HDPA for channel selection in LoRaWAN networks. The study began by identifying the limitations of static and non-learning-based channel selection mechanisms and emphasized the need for an adaptive solution in high-density and interference-heavy IoT environments.
The HDPA algorithms were theoretically formulated and tested through MATLAB simulations. The results confirmed that HDPA achieves faster convergence, higher channel selection accuracy (98.78%), and improved throughput over conventional models like HCPA. The HDPA model dynamically updates its channel selection probabilities in response to real-time feedback, making it particularly effective in environments where channel quality fluctuates.
These findings demonstrate that HDPA is a promising tool for optimizing LoRaWAN performance in both current and future IoT applications.
B. Future works
The successful integration of HDPA in this study opens an avenue for future research. One potential area is expanding the scope of Learning Automata to manage interference in densely populated IoT networks represents a critical research frontier. Future studies could also focus on real-world trials to better understand the practical challenges and opportunities of implementing these algorithms in diverse environments.
- Cheikh I, Sabir E, Aouami R, Sadik M, Roy S. Throughput-Delay Tradeoffs for Slotted-Aloha-based LoRaWAN Networks. In: 2021 International Wireless Communications and Mobile Computing (IWCMC); 2021 Jun 28–Jul 2; Harbin City, China. IEEE; 2021. Available from: https://doi.org/10.1109/IWCMC51323.2021.9498969
- Wang H, Pei P, Pan R, Wu K, Zhang Y, Xiao J, et al. A Collision Reduction Adaptive Data Rate Algorithm Based on the FSVM for a Low-Cost LoRa Gateway. Mathematics. 2022;10(21):3920. Available from: https://doi.org/10.3390/math10213920
- Zhang X, Jiao L, Granmo OC, Oommen BJ. Channel selection in cognitive radio networks: A switchable Bayesian learning automata approach. In: 2013 IEEE 24th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC); 2013 Sep 8–11; London, UK. IEEE; 2013. Available from: https://doi.org/10.1109/PIMRC.2013.6666540
- Diane A, Diallo O, Ndoye EHM. A systematic and comprehensive review on low-power wide-area network: characteristics, architecture, applications, and research challenges. Discov Internet Things. 2025;5(1):7. Available from: https://doi.org/10.1007/s43926-025-00097-6
- Bai RCAYJH. Evolutionary reinforcement learning: A survey. Intell Comput. 2023;2:0025. Available from: https://doi.org/10.34133/icomputing.0025
- Omslandseter RO, Jiao L, Zhang X, Yazidi A, Oommen BJ. The hierarchical discrete pursuit learning automaton: a novel scheme with fast convergence and epsilon-optimality. IEEE Trans Neural Netw Learn Syst. 2022;35(6):8278–8292. Available from: https://doi.org/10.1109/TNNLS.2022.3226538
- Yazidi A, Zhang X, Jiao L, Oommen BJ. The hierarchical continuous pursuit learning automation: a novel scheme for environments with large numbers of actions. IEEE Trans Neural Netw Learn Syst. 2019;31(2):512–526. Available from: https://doi.org/10.1109/TNNLS.2019.2905162
- Prakash A, Choudhury N, Hazarika A, Gorrela A. Effective Feature Selection for Predicting Spreading Factor with ML in Large LoRaWAN-based Mobile IoT Networks. In: 2025 National Conference on Communications (NCC); 2025 Feb 20–22; New Delhi, India. IEEE; 2025. Available from: https://doi.org/10.1109/NCC63735.2025.10983488
- Lavdas S, Bakas N, Vavousis K, Khalifeh A, Hajj WE, Zinonos Z. Evaluating LoRaWAN Network Performance in Smart City Environments Using Machine Learning. IEEE Internet Things J. 2025:1–1. Available from: https://doi.org/10.1109/JIOT.2025.3562222
- Garlisi D, Pagano A, Giuliano F, Croce D, Tinnirello I. Interference Analysis of LoRaWAN and Sigfox in Large-Scale Urban IoT Networks. IEEE Access. 2025;13:44836–44848. Available from: https://doi.org/10.1109/ACCESS.2025.3550014
- Keshmiri H, Emami R, Rezaee M, Wang A. LoRa Resource Allocation Algorithm for Higher Data Rates. Sensors. 2025;25(2):518. Available from: https://doi.org/10.3390/s25020518
- Li A, Fujisawa M, Urabe I, Kitagawa R, Kim SJ, Hasegawa M. A lightweight decentralized reinforcement learning based channel selection approach for high-density LoRaWAN. In: 2021 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN); 2021 Dec 13–15; Los Angeles, CA, USA. IEEE; 2021. Available from: https://doi.org/10.1109/DySPAN53946.2021.9677146
- Oyewobi SS, Hancke GP, Abu-Mahfouz AM, Onumanyi AJ. An effective spectrum handoff based on reinforcement learning for target channel selection in the industrial Internet of Things. Sensors. 2019;19(6):1395. Available from: https://doi.org/10.3390/s19061395
- Hasegawa S, Kim SJ, Shoji Y, Hasegawa M. Performance evaluation of machine learning based channel selection algorithm implemented on IoT sensor devices in coexisting IoT networks. In: 2020 IEEE 17th Annual Consumer Communications & Networking Conference (CCNC); 2020 Jan 10–13; Las Vegas, NV, USA. IEEE; 2020. Available from: https://doi.org/10.1109/CCNC46108.2020.9045712
- Loh F, Mehling N, Geißler S, Hoßfeld T. Simulative performance study of slotted Aloha for LoRaWAN channel access. In: NOMS 2022–2022 IEEE/IFIP Network Operations and Management Symposium; 2022 Apr 25–29; Budapest, Hungary. IEEE; 2022. Available from: https://doi.org/10.1109/NOMS54207.2022.9789898
- Yurii L, Anna L, Stepan S. Research on the Throughput Capacity of LoRaWAN Communication Channel. In: 2023 IEEE East-West Design & Test Symposium (EWDTS); 2023 Oct 6–8; Batumi, Georgia. IEEE; 2023. Available from: https://doi.org/10.1109/EWDTS59469.2023.10297024
- Gaillard G, Pham C. CANL LoRa: Collision Avoidance by Neighbor Listening for Dense LoRa Networks. In: 2023 IEEE Symposium on Computers and Communications (ISCC); 2023 Jul 3–6; Gammarth, Tunisia. IEEE; 2023. Available from: https://doi.org/10.1109/ISCC58397.2023.10218282
- LoRa Alliance. TS001-1.0.4 LoRaWAN L2 1.0.4 Specification. LoRa Alliance. 2020;1(0):4.