Multi-objective Particle Swarm Optimization: A Survey of the State-of-the-art

In the last decade, multi-objective particle swarm optimization (MOPSO) has been observed as one of the most powerful optimization algorithms in solving multi-objective optimization problems (MOPs). Nowadays, it is becoming increasingly clear that MOPSO can handle complex MOPs based on the competitive-cooperative framework. The goal of this paper is to provide a comprehensive review of MOPSO from the basic principles to hybrid evolutionary strategies. To offer the readers insights on the prominent developments of MOPSO, the key parameters on the convergence and diversity performance of MOPSO were analyzed to reflect the influence on the searching performance of particles. Then, the main advanced MOPSO methods were discussed, as well as the theoretical analysis of multi-objective optimization performance metrics. Even though some hybrid MOPSO methods show promising multi-objective optimization performance, there is much room left for researchers to improve further, in particular in terms of engineering applications. As a result, further in-depth studies are required. This paper should motivate evolutionary computation researchers to pay more attention to this practical yet challenging area.

Most of the practical engineering application problems, such as electrical and electronic engineering problems, civil engineering problems, are Multi-objective Optimization Problems (MOPs) [1]. MOPs not only contain multiple conflicting objectives simultaneously, but the objectives are usually time-varying and coupled with each other. The presence of multiple conflicting objectives can give rise to a set of trade-off solutions known as Pareto Front in the objective space and Pareto Set in the decision space, respectively [2]. Since it is practically impossible to obtain the entire Pareto Front solutions, an approximation of non-dominated solutions can be obtained. The original multi-objective optimization approaches are usually based on transforming the MOP to several single objectives by different weight methods and then obtaining a set of non-dominated optimal solutions. Therefore, traditional optimization methods have many drawbacks, such as high computational complexity and long time, so they cannot meet the requirements of speed, convergence, and diversity [3].

Generally speaking, to obtain an accurate solution set when solving the complex MOPs, researchers draw lessons from the laws of nature and biology to design a class of Multi-objective Evolutionary Algorithms (MOEAs) to improve the convergence accuracy. As an important field of artificial intelligence, MOEA has made many breakthroughs in algorithm theory and algorithm performance, because of its characteristics of intelligence and parallelism. It has played an important role in scientific research and production practice. During the last two decades, MOEA has become a new research direction, because it has better global search ability and does not rely on a specific mathematical model and characteristics of solving the problem when solving the multi-objective optimization problem [4,5]. The performance of MOEAs is mainly evaluated by a set of non-dominated solutions obtained by the performance metrics, including the convergence metric and diversity metric. In general, the typical MOEAs include the multi-objective genetic algorithm (MOGA) [6], the Multi-objective Differential Evolution (MODE) algorithm [7], and so on [8-10]. It is precisely this way that deepening the research of computational intelligence algorithms can promote the development of intelligent technology and promote innovation in many fields. Distinguishingly, the multi-objective particle swarm optimization (MOPSO) algorithm based on the bird population shows complex intelligent behavior through the cooperation of simple individual particles, and uses social sharing among the bird population to promote the evolutionary process of the algorithm. Therefore, MOPSO realizes the transcendence of the swarm intelligence that can exceed the outstanding individual particle intelligence [11]. Meanwhile, due to the few key operation parameters, high convergence speed, and ease of implementation, MOPSO can handle many kinds of objective functions and constraints.

In the MOPSO community, the key parameters can impact the exploitation ability and exploration ability in the searching process of particles [12]. Meanwhile, different updating methods will guide the particles to search different areas and then affect the performance of the whole population. With the increasing number of iterations, more and more non-dominated solutions will be generated [13]. As the amount of calculation increases, the archive cannot accommodate the whole non-dominated solutions [14]. The convergence and diversity of the non-dominated solutions in the archive will become important. In order to reach good convergence and diversity of the non-dominated in the archive, the three main optimization stages, which include the update of the archive, the selection of the global best, and the key flight parameter adjustment, will be considered. Like all MOEAs, MOPSO also needs an explicit diversity mechanism to preserve the non-dominated solutions in the archive. In [15], a selection procedure was proposed to prune the non-dominated solutions. In order to obtain a good diversity of the archive, a novel reproduction operator based on differential evolution was presented, which can create potential solutions and accelerate the convergence toward the Pareto set [16]. The MOPSO emerged as a competitive and cooperative form of evolutionary computation in the last decade. One of the most special features of MOPSO is the updating of the global best (g-Best) and personal best (p-Best) [17,18]. Aiming at the selection of the g-Best and p-Best, a novel Parallel Cell Coordinate System (PCCS) is proposed to accelerate the convergence of MOPSO by assessing the evolutionary environment [19]. Another important feature is the parameter adjustment; for example, the inertia weight can achieve the balance of exploration and exploitation. And the coefficients adjustment can also influence movement of the particle. In [20], a time-varying flight parameter mechanism was proposed for the MOPSO algorithms. At present, there are many performance metrics in multi-objective optimization to determine the convergence and diversity of MOPSO. The main performance metrics of MOPSO contain the determination of convergence and diversity. Meanwhile, different application environments of MOPSO will consider different performance metrics and impact the future development trend.

At present, especially in the complex science field, MOPSO has effectively solved problems which is difficult to describe in many complex systems. It breaks through the limitations of the traditional multi-objective optimization algorithm, and has been used in many applications in various academic and industrial fields so far [21]. MOPSO has made encouraging progress in many applications in various academic and industrial fields so far, which is including the automatic control system [22], communication theory [23], medical engineering [24], electrical and electronic engineering [25], communication theory [26], fuel and energy [27], and so on.

1. Different from the cross mutation operation of other optimization algorithms, MOPSO is much simpler and straightforward to implement. As an MOEA based on a bird group, MOPSO shows complex intelligent behavior through the cooperation of simple individual particles, and uses social sharing among groups to promote the evolutionary process of the algorithm. Therefore, realizing the breakthrough of swarm intelligence on MOPSO that can exceed the excellent individual particle intelligence.
2. As indicated by the current studies on MOPSO, it has few key parameters. It can be seen from the updating formula of the MOPSO algorithm that the position and speed of the particle are greatly influenced by the key parameters. The convergence of the algorithm is the fundamental guarantee of its application. The effect of the key parameters of the MOPSO algorithm on the convergence of the algorithm is analyzed in detail, and the flight direction of the particles is calculated by the state transfer matrix. The constraint condition [28] that satisfies the parameters of particle trajectory is obtained.
3. Compared with other MOEAs, the fast convergence is a typical characteristic of MOPSO. Since the flight direction of MOPSO can be obtained by the g-Best and p-Best of the population, the whole particle swarm is easy to gather or disperse. Therefore, the convergence rate of MOPSO will be relatively faster than other MOEAs.

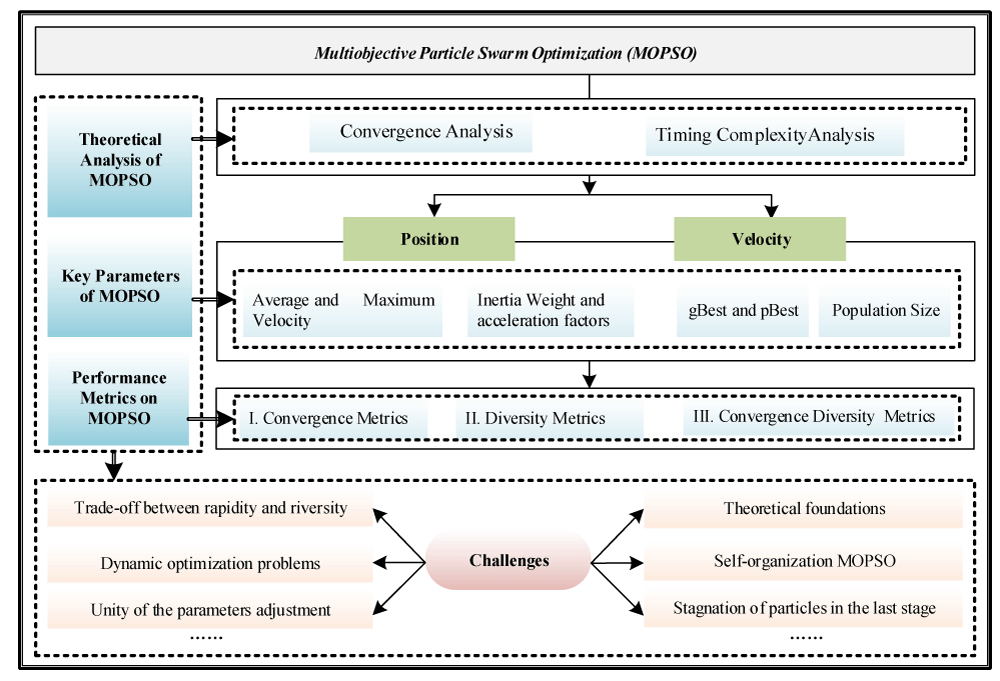
In order to make a summary of the work in the last two decades, we discussed the achievements and the direction of development and wrote this review article. This paper attempts to provide a comprehensive survey of MOPSO. The major scheme of this paper is shown in Figure 1. Section II briefly describes the basic concepts and key parameters of MOPSO. In Section III, the improved approaches of MOPSO by different performance metrics are presented, and the theoretical analysis of MOPSO is presented. Then, Section IV gives the potential future research challenges of MOPSO. Finally, the paper is concluded in Section V.

Faced with the complex MOPs in practical application, the traditional optimization method has the problems of high computational complexity and long time, which cannot meet the requirements of computing speed, convergence, diversity, and so on. In order to solve the complex MOPs better, scientists draw lessons from the laws of nature and biology to design a computational intelligence algorithm for solving the problem. As an important field of artificial intelligence, computational intelligence algorithms have made many breakthroughs in algorithm theory and algorithm performance because of their characteristics of intelligence and parallelism. However, the MOPSO algorithm is a typical computational intelligence algorithm with strong optimization ability. It has been able to solve the multi-objective optimization problem, which is difficult to establish accurate models in many complex systems.

A. Basic Concept of MOPSO

MOPSO is a population-based optimization technique, in which the population is referred to as a swarm. A particle has a position which is represented by a vector:

$x_i(t)=[x_{i,1}(t),x_{i,2}(t),\mathrm{....}{x}_{i,D}(t)],$ (3)

where D is the dimension of the search space, i=1, 2, …, S, S is the size of the swarm. And each particle has a velocity which is recorded as:

$v_i(t)=[v_{i,1}(t),v_{i,2}(t),\mathrm{....}{v}_{i,D}(t)],$ (4)

In the evolutionary process, p_i(t) is the best previous position of the particle at the tth iteration which is recorded as p_i(t)=[p_i,1(t), p_i,2(t),…, p_i, D(t)], and g-Best(t) is the best position found by the swarm which is recorded as g-Best(t)=[g-Best1(t), g-Best2(t),…, g-Best D(t)]. A global best solution, g-Best, can be found by the whole particle swarm. In each iteration, the velocity is updated by:

$v_{i,d}(t+1)=\omega v_{i,d}(t)+c_1{r}_1(p_{i,d}(t)-x_{i,d}(t)+c_2{r}_2(g{\text{Best}}_d(t)-x_{i,d}(t)),$ (5)

where i=1, 2, …, s, t represents the tth iteration in the evolutionary process; d=1, 2, …, D represents the dth dimension in the searching space; ɷ is the inertia weight, which is used to control the effect of the previous velocities on the current velocity; c₁ and c₂ are the acceleration constants, r₁ and r₂ are the random values uniformly distributed in [0, 1]. Then the new position is updated as (Table 1):

$x_{i,d}(t+1)=x_{i,d}(t)+x_{i,d}(t+1).$ (6)

Remark 1: MOPSO is a population-based evolutionary algorithm that is inspired by the social behavior of the birds’ flocking motion, which has been steadily gaining attention from the research community because of its high convergence speed. The aggregate motion of the whole particles formed the searching movement of the MOPSO algorithm. Like other evolutionary algorithms, MOPSO suffers from a notable bias: it tends to perform best when the optimum is located at or near the center of the initialization region, which is often the origin.

In MOPSO, particles move through the search space using an information interaction between particles, and each particle is attracted by the personal and global best solutions to move toward their potential leader. Particles can be connected in any kind of neighborhood topology, which contains the ring neighborhood topology, the fully connected neighborhood topology, the star network topology, and the tree network topology. For instance, due to the fully connected topology in which all particles are connected, each particle can receive the information of the best solution from the whole swarm at the same time. Thus, when using the fully connected topology, the swarm is inclined to converge more rapidly than when using other local best topologies [29].

Remark 2: In the searching process of an MOPSO algorithm, when convergence is considered separately, it may lead to a local optimal trap. If diversity is considered separately, the convergence speed and quality will be an unsolved problem. In the optimization process of MOPSO algorithm, many optimization patterns could exert an influence on the optimization results, in terms of leader selection, archive maintenance, flight parameter adjustment, population size, and perturbation. Therefore, these several important aspects will become the key means to improve the optimization effect. The leader selection affects the convergence capability and the distribution of non-dominated solutions along the Pareto Front.

B. Key Parameters of MOPSO

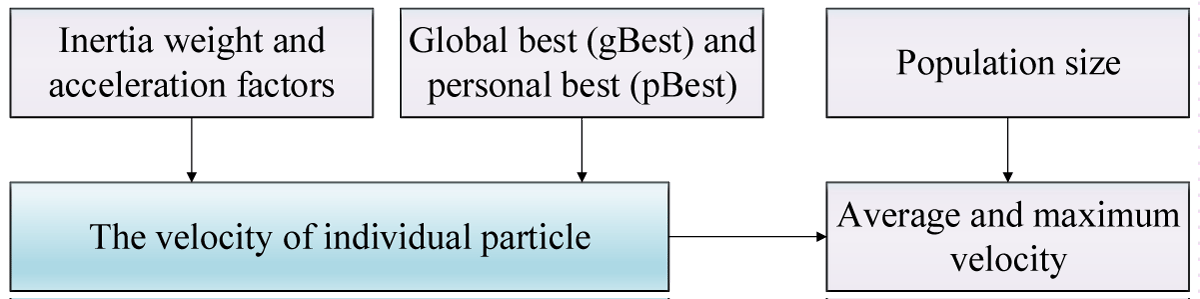
The relationship between the key parameters is depicted in Figure 2.

(a) Average and maximum velocity

MOPSO algorithm makes full use of shared learning factor to modify the velocity updating formulas, which aims to improve the global search ability [30]. The optimal value of maximum velocity is problem-specific. Further, when maximum velocity was implemented, the particle’s trajectory failed to converge. From the velocity updating formula of the particle, it can be seen that the velocity of the particle is subjected to the key parameters (ω, c₁, and c₂) of the particles. The contribution rate of a particle’s previous velocity to its velocity at the current time step is determined by the key parameters [31]. It is necessary to limit the maximum velocity. For example, if the velocity is very large, particles may fly out of the search space and decrease the searching quality of the MOPSO algorithm. In contrast, if the velocity is very small, particles may become trapped in the local optimum. In order to hinder too quick movement of particles, their velocities are bounded to specified values [32].

(b) Inertia weight and acceleration factors

From the flight equations, it is clearly shown that the new position of each particle is affected by the inertia weight ω and two cognitive acceleration coefficients c₁ and c₂. The acceleration coefficient c1 prompts the attraction of the particle towards its p-Best, and the acceleration coefficient c₂ prompts the attraction of the particle towards the g-Best. The parameter inertia weight ω helps the particles converge to personal and global best, rather than oscillating around it. The inertia weight controls the influence of previous velocities on the new velocity [31].

Too high values of cognitive acceleration coefficient weaken exploration ability, while too high values of social acceleration coefficient lead to weak exploitation capability [32]. Therefore, suitable cognitive acceleration coefficients are very important for the optimization process of an MOPSO algorithm. Most of the prior research has indicated that the inertia weight ω controls the impact of the previous velocity on the current velocity, which is employed to trade off between the global and local exploration abilities of the particles [30]. Moreover, the purpose of designing the adaptive inertia weight is to balance the global and local search ability of the particles. Most previous works have demonstrated that a larger inertia weight ω facilitates global exploration, while a small inertia weight tends to facilitate local exploration to guide the current search area. Suitable selection of inertia weight ω can provide balance between global and local exploration abilities and thus require fewer iterations on average to find the optimum. In the previous research, different inertia weight mechanisms have been designed to balance the global searching ability and the local searching ability, where the inertia weight was adjusted dynamically to adapt the optimization process.

(c) Global best (g-Best) and personal best (p-Best)

In MOPSO, each particle moves toward the most promising directions guided by the g-Best and the p-Best together, and the whole population follows the trajectory of g-Best [33]. The g-Best and the p-Best can guide the evolutionary direction of the whole population. In addition, the updating formula of the MOPSO algorithm has illustrated that the value of the g-Best and the p-Best can play an important role in the updating of the velocity and position. In the searching process, selecting the appropriate g-Best and the p-Best in MOPSO is a feasible way to control its convergence and promote its diversity. In recent years, the popular issue of Best selection is keeping the balance of convergence and diversity. Some researchers have proposed adaptive selection mechanisms that select the g-Best with convergence and diversity features in the dynamic evolutionary environment.

(d) Population size

The population size of the MOPSO does indirectly contribute to the effectiveness and efficiency of the performance of an algorithm [34]. One contribution of population size to these population-based evolutionary algorithms is the computational cost.

In the searching process, if an algorithm employs an overly large population size, it will enjoy a better chance of exploring the search space and discovering possible good solutions, but inevitably suffer from an undesirable and high computational cost. In contrast, an MOPSO algorithm with an insufficient population size may become trapped in premature convergence or may obtain the solution archive with a loss of diversity.

The external archive can store a certain number of non-dominated solutions, which determine the convergence and diversity performance of MOPSO. Although there are many external archive strategies that have been proposed, several strategies can achieve a good balance between diversity and convergence. In addition, the research on the external archive strategies is still necessary to improve the performance of MOPSO as a whole. On one hand, diversity is one of the most characteristic features in the external archive of MOPSO, which reflects the validity of the MOPs to be solved. On the other hand, convergence is another criterion to judge the performance of MOPSO and its approach to the true Pareto Front.

Remark 3: The convergence and diversity are two principles for evaluating the performance of MOPSO. Meanwhile, the adjustments of the key parameters can affect the flight direction of particles and then obtain different optimization performance. However, the performance metrics have been designed with different standpoints to evaluate the performance of MOPSO. Three typical performance criteria have been considered in multi-objective optimization: 1) the number of non-dominated solutions. 2) the convergence of non-dominated solutions to the Pareto Front. 3) the diversity of non-dominated solutions in the objective space. In particular, a set of optimal non-dominated solutions with best convergence and diversity, which are approaching the true Pareto Front and scattering evenly, is generally desirable.

In the multi-objective optimization performance metrics, two major performance criteria, namely, convergence and diversity, have typically been taken into considerations. Based on the convergence and diversity performance of MOPSO, the existing improved approaches categorized into three groups.

1. Diversity metrics: These metrics contain two aspects: a) Distribution measures whether evenly scattered are the optimal non-dominated solutions, and b) spread demonstrates whether the optimal non-dominated solutions approach the extrema of the Pareto Front.
2. Convergence metrics: These metrics can measure the degree of approximation between the optimal non-dominated solutions by the proposed MOPSO and the true Pareto Front.
3. Convergence-diversity metrics: These metrics can both indicate and measure the convergence and diversity of the optimal non-dominated solutions.

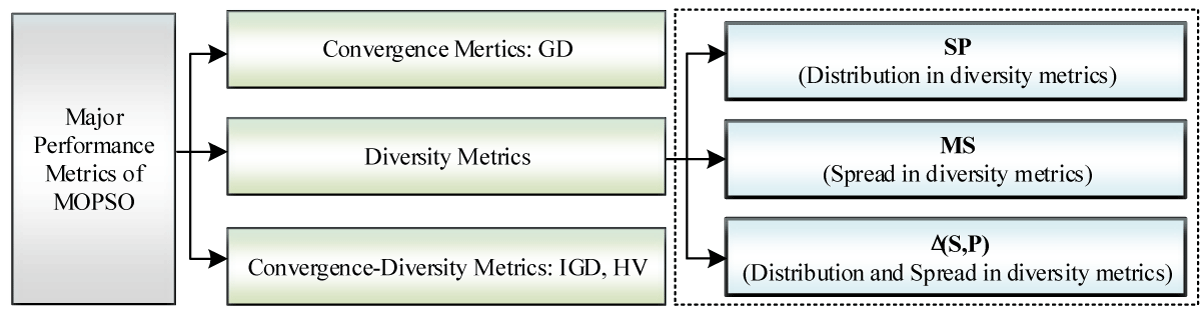
According to the above-mentioned analysis, the major performance metrics of MOPSO are shown in Figure 3.

A. Diversity metrics

Diversity metrics demonstrate the distribution and spread of the solutions in the archive.

(a) Distribution in diversity metrics

The distribution quality of the non-dominated solutions in the archive is an important aspect to reflect the diversity performance of the MOPSO algorithm.

The spacing (SP) metric: The distribution is derived from the non-dominated solutions in the archive, which is defined as:

$SP(S)=\sqrt{{\displaystyle {\sum }_{i=1}^{\left|s\right|}{(d_i-\overline{d})}^2/(\left|S\right|-1)}},$ (7)

Where $d_i=\underset{\overrightarrow{s_j}\in S,\overrightarrow{\overrightarrow{s_i}\ne \overrightarrow{s_j}}}{\min }\Vert F(\overrightarrow{s_i})-F(\overrightarrow{s_j})\Vert {\overrightarrow{s}}_i\in S$ . D_i is the minimum Euclidean distance between the solution ${\overrightarrow{s}}_j\in S.$ and the solutions ${\overrightarrow{s}}_j\in S.$ $$\overline{d}$$ Is the average Euclidean distance of all the distances. If the value of SP is larger, it will represent a poor distribution of diversity. On the contrary, the smaller SP can indicate the MOPSO algorithm with good distribution performance.

SP is used to measure the spread of vectors throughout the non-dominated vectors found so far. Since the “beginning” and “end” of the current Pareto front are known, a suitably defined metric judges how well the solutions in such a front are distributed. A value of zero for this metric indicates all members of the Pareto front currently available are equidistantly spaced. This metric addresses the second issue from the list previously provided.

The $M_2^{*}(S)$ Metric in [35] is equipped with a niche radius σ and takes the form of

$M_2^{*}(S)=\frac{{\displaystyle {\sum }_{\overrightarrow{s_1}\in S}\left|\{\overrightarrow{s_2}\in S|\Vert \overrightarrow{s_1}-\overrightarrow{s_2}\Vert <\sigma \}\right|}}{\left|S\right|-1},$ (8)

where measures how many solutions.. They are located in their local vicinity. σ is a niche radius. Note that a niche neighboring size is needed to calculate the distribution of the non-dominated solution. The higher the value the MOPSO algorithm can obtain a good distribution of the non-dominated solutions.

a) Increasing the diversity of the non-dominated solutions in the archive

Raquel, et al. presented an extended approach by incorporating the mechanism of crowding distance computation into the developed MOPSO algorithm to handle the MOPs, where the global best selection and the deletion method of the external archive have been used. The results show that the proposed MOPSO algorithm can generate a set of uniformly distributed non-dominated solutions close to the Pareto Front [36].

Coello, et al. proposed an external repository strategy to guide the flight direction of particles, which includes the archive controller and an adaptive grid [20]. The archive controller is designed to control the storage of non-dominated solutions in the external archive, and the adaptive grid is used to distribute in a uniform way to obtain the largest possible amount of hypercubes. The external repository strategy also incorporates a special mutation operator method which improves the exploratory capabilities of the particles and enriches the diversity of the MOPSO algorithm. Moreover, Moubayed, et al. developed a MOPSO by incorporating dominance with decomposition (D2MOPSO), which employs a new archiving technique that facilitates attaining better diversity and coverage in both objective and solution spaces [37].

Agrawal, et al. proposed a Fuzzy Clustering-based Particle Swarm Optimization (FCPSO) algorithm to solve the highly constrained conflicting multi-objective problems. The results indicated that it generated a uniformly distributed Pareto front whose optimality has been proved greater than ε-constrainted method [38].

A multi-objective particle swarm optimization is proposed in [39], which uses a fitness function derived from the maximin strategy to determine Pareto-domination. The results show that the proposed MOPSO algorithm produces an almost perfect convergence and spread of solutions towards and along the Pareto Front.

b) The inertia weight adjustment mechanisms improved the global exploration ability

Daneshyari, et al. introduced a cultural framework to design a flight parameter mechanism for updating the personalized flight parameters of the mutated particles in [40]. The results show that this flight parameter mechanism performs efficiently in exploring solutions close to the true Pareto front. In addition, a parameter control mechanism was developed to change the parameters for improving the robustness of MOPSO.

c) Selecting the proper g-Best and p-Best with better diversity

Ali, et al. introduced an attributed MOPSO algorithm, which can update the velocity of each dimension by selecting the g-Best solutions from the population [41]. The experiments indicate that the attributed MOPSO algorithm can improve the search speed in the evolutionary process. In [42], a multi-objective particle swarm optimization with preference-based sort (MOPSO-PS), in which the user’s preference was incorporated into the evolutionary process to determine the relative merits of non-dominated solutions, was developed to choose the suitable g-Best and p-Best. After each optimization, the most preferable particle can be chosen as the g-Best by the selection of the highest global evaluation value.

Zheng, et al. introduced a new MOPSO algorithm, which can maintain the diversity of the swarm and improve the performance of the evolving particles significantly over some state-of-the-art MOPSO algorithms by using a comprehensive learning strategy [43]. Torabi, et al. introduced an efficient MOPSO with a new fuzzy multi-objective programming model to solve an unrelated parallel machine scheduling problem. The proposed MOPSO exploits a new selection regime for preserving global best solutions and obtains a set of non-dominated solutions with good diversity [44].

d) Dividing the particle population into multiple groups

Zhang, et al. introduced an enhanced problem-specific local search technique (MO-PSO-L) to seek high-quality non-dominated solutions. The local search technique has been specifically designed for searching more potential non-dominated solutions in the vacant space. The computational experiments have verified that the proposed MO-PSO-L can deal with complex MOPs [45].

The effective archive strategy can generate a group of uniformly distributed non-dominant solutions and can accurately approach the Pareto frontiers. At the same time, the effective archive strategy can guide the direction of the particle flight. The external knowledge base strategy also contains a special mutation operator method, which can improve the searching ability of the particles. In order to balance the global exploration ability and the local exploitation ability of the particle, the time-varying flight parameter mechanism can update the flight parameters by iteration and adjust the value of the inertia weight. It can strengthen the global searching ability of the algorithm and obtain more optimal solutions. For multiple constrained multi-objective conflicting problems, the clustering method is used to divide the non-dominant solutions in the archive into multiple subgroups, which can enhance the local search performance of each subgroup. The dominating relationship is determined by calculating the fitness value of the target function, so that the non-dominant solution in the archive can be distributed evenly.

(b) Spread in diversity metrics

The spread of diversity is another typical aspect to reflect the diversity performance of MOPSO algorithms.

The maximum spread (MS) metric: The spread quality of the non-dominated solutions in the archive can also represent the diversity, and MS is defined as:

$\mathrm{MS}=\sqrt{\frac{1}{N}{\displaystyle \sum _{i=1}^N{[\frac{\min (f_i^{\max }-F_i^{\max })-max(f_i^{\min }-F_i^{\min })}{F_i^{\max }-F_i^{\min }}]}^2}}$ (9)

Where F_i^max is the maximum value of the _ith objective in Pareto Front, F_i^min is the minimum value of the _ith objective in Pareto Front. F_i^max is the maximum value of the _ith objective in the solution archive; F_i^min is the minimum value of the _ith objective in the solution archive. Most of the previous work shows that the larger MS, the better spread of diversity will be obtained by the evolutionary algorithm in the archive.

The maximum spread is conceived to reveal how well obtained optimal solutions cover the true Pareto front. The larger the MS value is, the better the obtained optimal solutions cover the true Pareto front. The limiting value MS=1 means that the obtained optimal solutions cover completely the true Pareto front.

a) Selecting the proper g-Best and p-Best with better diversity

Shim, et al. proposed an estimation distribution algorithm to model the global distribution of the population for balancing the convergence and diversity of the MOPSO algorithms [46]. The results indicate that this method can improve the convergent speed.

Multimodal multi-objective problems are usually posed as several single-objective problems that sometimes include more than one local optimum or several global optima. To handle the multimodal multi-objective problems effectively, Yue, et al. proposed a multi-objective particle swarm optimizer using an index-based ring topology to maintain a set of non-dominated solutions with good distribution in the decision and objective spaces [47]. Further, the experimental results show that the proposed algorithm can obtain a larger MS value and has made great progress on solving the decision space distribution.

b) Increasing the diversity of the non-dominated solutions in the archive

Huang, et al. proposed a multi-objective comprehensive learning particle swarm optimizer (MOCLPSO) algorithm by integrating an external archive technique to handle MOPs. Simulation results show that the proposed MOCLPSO algorithm can find a much better spread of solutions and faster convergence to the true Pareto Front [48].

(c) Distribution and spread in diversity metrics

The metric Δ is introduced in [6], which is considered to reflect the distribution and spread of the non-dominated solutions in the archive simultaneously. The formulation of Δ is derived as follows:

$\Delta (S,P)=\frac{d_f+d_l+{\displaystyle {\sum }_{i=1}^{\left|S\right|-1}\left|d_i-\overline{d}\right|}}{d_f+d_l+(\left|S\right|-1)\overline{d}},$ (10)

where d_i is the Euclidean distance between consecutive solutions. And it is the average of all. d_f and d₁ are the minimum Euclidean distances between the extreme solutions in the true Pareto Front and the boundary solutions of the non-dominated solutions in the archive. S is the capacity of the archive.

In order to increase the diversity for dealing with MOPs, Tsai, et al. proposed an improved multi-objective particle swarm optimizer based on Proportional Distribution and Jump Improved Operation (PDJI-MOPSO). The proposed PDJI-MOPSO maintains diversity of newly found non-dominated solutions via proportional distribution and obtains extensive exploitation of the MOPSO algorithm in the archive with the jump improved operation to enhance the solution searching abilities of particles [49].

a) Increasing the diversity of the non-dominated solutions in the archive

Cheng, et al. proposed a hybrid MOPSO with local search strategy (LOPMOPSO), which consists of the quadratic approximation algorithm and the exterior penalty function method. The dynamic archive maintenance strategy is applied to improve the diversity of solutions, and the experimental results show that the proposed LOPMOPSO is highly competitive in convergence speed and generates a set of non-dominated solutions with good diversity [50]. Ali, et al. proposed an Attributed Multi-objective Comprehensive Learning Particle Swarm Optimizer (A-MOCLPSO), which optimizes the total security cost and the residual damage. The experimental results show that the proposed A-MOCLPSO algorithm can provide diverse solutions for the problem and outperform the previous solutions obtained by other comparable algorithms [51].

In order to effectively deal with the multimodal and complex MOPs, a group of non-dominated solutions with good distribution can be obtained by changing the information sharing mode between particles in the decision and objective space, and great progress has been made in solving the distribution of decision space. Given multimodal problems and MOPs in a noisy environment, it is necessary to consider the extension of the MOPSO algorithm and analyze the MS metric.

B. Convergence metrics

Convergence metrics measure the degree of proximity, which is the distance between the non-dominated solutions and the Pareto Front.

The Generational Distance (GD) metric: The essence of GD is to calculate the distance between the non-dominated solution in the archive and the true Pareto Front, which is defined as:

$\mathrm{GD}(S,P)=\frac{{({\displaystyle {\sum }_{i=1}^{\left|s\right|}{d}_i^q})}^{1/q}}{\left|S\right|},$ (11)

where a finite number of the non-dominated solutions that approximate the true Pareto Front is called P, the optimal non-dominated solution archive obtained by the evolutionary algorithms is termed as S. |S| is the number of non-dominated solutions in the archive $d_i=\underset{\overrightarrow{p}\in P}{\min }\Vert F(\overrightarrow{s_i})-F(\overrightarrow{p})\Vert ,{\overrightarrow{s}}_j\in S.$ . and q=2, di is the minimum Euclidean distance between the solution $\overrightarrow{s}$ ∈S and the solutions in P. In essence, GD can reflect the convergence performance of the MOPSO algorithm.

GD illustrates the convergence ability of the algorithm by measuring the closeness between the Pareto optimal front and the evolved Pareto front. Thus, a lower value of GD shows that the evolved Pareto front is closer to the Pareto optimal front. It should be clear that a value of indicates that all the elements generated are in the Pareto optimal set. Therefore, any other value will indicate how “far” we are from the global Pareto front of our problem. This metric addresses the first issue from the list previously provided.

(a) The inertia weight adjustment mechanisms improved the local exploitation ability.

Tang, et al. introduced a self-adaptive PSO (SAPSO) based on a parameter selection principle to guarantee convergence when handling the MOPs. To gain a well-distributed Pareto front, an external repository was designed to keep the non-dominated solutions with good convergence. The statistical results of GD have illustrated that the proposed SAPSO can obtain a set of non-dominated solutions close to the Pareto Front [52].

(b) Speeding up the convergence by the external archive

Zhu, et al. introduced a novel external archive-guided MOPSO (AgMOPSO) algorithm, where the leaders for velocity updating and position updating are selected from the external archive [53]. In AgMOPSO, MOPs are transformed into a set of sub-problems, and each particle is allocated to optimize a sub-problem. Meanwhile, an immune-based evolutionary strategy of the external archive increased the convergence to the Pareto Front and accelerated the rate. Different from the existing algorithms, the proposed AgMOPSO algorithm is devoted to exploiting the useful information fully from the external archive to enhance the convergence performance. In [33], a novel parallel cell coordinate system (PCCS) is proposed to accelerate the convergence of MOPSO by assessing the evolutionary environment. The PCCS has transformed the multi-objective functions into two-dimensional space, which can accurately grasp the distribution of the non-dominated solutions in high-dimensional space. An additional experiment for density estimation in MOPSO illustrates that the performance of PCCS is superior to that of adaptive grid and crowding distance in terms of convergence and diversity.

Wang, et al. developed a multi-objective optimization algorithm with the preference order ranking of the non-dominated solutions in the archive [54]. And the experimental results indicated that the proposed algorithm improves the exploratory ability of MOPSO and converges to the Pareto Front effectively.

(c) Selecting proper g-Best and p-Best

Alvarez, et al. developed an MOPSO algorithm using exclusively on dominance for selecting guides from the solution archive to find a more feasible region and explore regions close to the boundaries. The results demonstrate that the proposed algorithm can shrink the velocity of the particles, and the particles can fly to the boundary of the true Pareto Front, which has a good GD value [55].

Wang, et al. developed a new ranking scheme based on equilibrium strategy for MOPSO algorithm to select the g-Best in the archive, and the preference ordering is used to decrease the selective pressure, especially when the number of objectives is very large. The experimental results indicate that the proposed MOPSO algorithm produces better convergence performance [56].

(d) Adjusting the population size

A multiple-swarm MOPSO algorithm, named dynamic multiple swarms in MOPSO, is proposed in which the number of swarms is dynamic in the searching process. Yen, et al. proposed a dynamic multiple swarms in MOPSO (DSMOPSO) algorithm to manage the communication within a swarm and among swarms, and an objective space compression and expansion strategy to progressively exploit the objective space during the search process [57]. The proposed DSMOPSO algorithm occasionally exhibits slower search progression, which may render a larger computational cost than other selected MOPSOs.

In order to solve the application problem with the increasing complexity and dimensionality, Goh, et al. developed an MOPSO algorithm with a competitive and cooperative co-evolutionary approach, which divides the particle swarms into several sub-swarms [58]. Simulation results demonstrated that the proposed MOPSO algorithm can retain the fast convergence speed to the Pareto Front with a good GD value.

(e) Hybrid MOPSO algorithms

In order to increase the convergence accuracy and the speed of the MOPSO algorithm, MOPSO is combined with other intelligent algorithms. In [59], an efficient MOPSO algorithm based on the strength Pareto approach from EA was developed. The experimental results show that the proposed MOPSO algorithm can converge to the Pareto Front and has a slower convergence time than SPEA2 and a competitive MOPSO algorithm. MOPSO can also combine with other global optimization algorithms. The evaluation of GD index is relatively simple, mainly considering the distance between all non-dominated solutions in the external archive and the frontier, but it cannot provide diversity information.

C. The evaluation of GD metric is relatively simple, which mainly considers the distance between all non-dominated solutions and the Pareto front in the archive, but it can not provide diversity. Because the calculation of the GD metric needs the real Pareto front, but the actual problem often has no real Pareto front, so its use will be limited. However, for the multi-objective optimization problem of the known front, it is suitable for MOPs with strict convergence when handling the actual problems.

C. Convergence-diversity metrics

The aim of optimizing MOPs is to obtain a set of uniformly distributed non-dominated solutions that is close to the true Pareto Front. In order to evaluate the optimal solutions in the archive, two performance metrics are applied to measure the MOPSO algorithm, which can reflect both the convergence and diversity performance.

The inverted generational distance (IGD) metric: IGD is used to compare the disparity between the non-dominated solutions by the optimization algorithm and the true Front, which is defined as:

$I\mathrm{GD}(P,S)=\frac{{({\displaystyle {\sum }_{i=1}^{\left|P\right|}{d}_i^q})}^{1/q}}{\left|P\right|},$ (12)

where a finite number of the non-dominated solutions that approximate the true Pareto Front is called P, the optimal non-dominated solution archive obtained by the evolutionary algorithms is termed as S. |P| is the number of non-dominated solutions in the Pareto Front. $d_i=\underset{\overrightarrow{s}\in S}{\min }\Vert F(\overrightarrow{p_i})-F(\overrightarrow{s})\Vert {\overrightarrow{p}}_i\in p.$ and q=2, d_i is the minimum Euclidean distance between the solution $\overrightarrow{s}\in s.$ and the solutions $\overrightarrow{p}\in p$ . In particular, the smaller value of IGD means that the non-dominated solutions in the archive are closer to the true Pareto Front.

IGD performs the near calculation similar to that done by GD. The difference is that GD calculates the distance of each solution in optimal solutions to the Pareto Front, while IGD calculates the distance of each solution in the Pareto Front to optimal solutions. In this indicator, both convergence and diversity are taken into consideration. A lower value of IGD implies that the algorithm has better performance.

The hypervolume (HV) metric: HV is another popular convergence–diversity metric to evaluate the volume of the non-dominated solutions in the archive concerning the reference set.

$\mathrm{HV}(S,R)=volume(\underset{i=1}{\overset{\left|S\right|}{{\displaystyle \cup }}}{v}_i),$ (13)

where R is the reference set. $\overrightarrow{s}\in s.$ , a hypercube v_i is formed by the reference set and the solution as the diagonal corners of the hypercube. When the non-dominated solutions in the archive are closer to the Pareto Front, a larger HV can demonstrate that solutions in the archive are more uniformly distributed in the objective space.

In order to assess the performance among different compared algorithms, two performance measures, i.e., IGD and HV, were adopted here. It is believed that these two performance indicators can not only account for convergence, but also the distribution of final solutions.

b) Adjusting the population size

Leong, et al. presented a dynamic population multiple-swarm MOPSO algorithm to improve the diversity within each swarm, which included the integration of a dynamic population strategy and an adaptive local archive. The experimental results indicated that the proposed MOPSO algorithm shows competitive results with improved diversity and convergence and demands less computational cost [34].

In actual industrial problems, there are many many-objective problems (MaOP) and optimization algorithms aimed at searching for a set of uniformly distributed solutions that closely approximate the Pareto Front. In [60], Carvalho, et al. proposed a many-objective technique named control of dominance area of solutions (CDAS), which is used on three different many-objective particle swarm optimization algorithms. Most previous studies only deal with rank-based algorithms. The proposed CDAS technique for the MOPSO algorithm that are based on the cooperation of particles, instead of a competitive method. Wang, et al. proposed a hybrid evolutionary algorithm by the MOEA and MOPSO to balance the exploitation and exploration of the particles. The whole population is divided into several sub-populations to solve the scalar sub-problems from an MOP [61]. The comprehensive experiments with respect to IGD metric and HV metric can indicate that the performance of the proposed method is better than other comparable MOEAs.

c) Increasing the diversity of the non-dominated solutions in the archive

In general, the MOPSO algorithm will scale poorly when the number of objectives is more than three. To solve this problem, Britto, et al. proposed a novel archiving MOPSO algorithm to explore more regions of the Pareto Front which applying the reference point to update the archive [62]. The empirical analysis of the proposed MOPSO algorithm verified the distribution of the solutions and experimental results, showing that the solutions generated by this algorithm could be very close to the reference point.

d) The inertia weight adjustment mechanisms improved the global exploration ability

Sorkhabi, et al. presented an efficient approach to constraint handling in MOPSO, and the whole population is divided into two non-overlapping populations, which include the infeasible particles and feasible particles. Meanwhile, the leader is selected from the feasible population. The experimental results demonstrated that the proposed algorithm is highly competitive in solving the MOPs. Meza, et al. proposed a multi-objective vortex particle swarm optimization (MOVPSO) based on the emulation of the particles. The qualitative results show that the MOVPSO algorithm can have a better performance compared to the traditional MOPSO algorithm [35]. Zhang, et al. proposed a competitive MOPSO, where the particles are updated on the basis of the pairwise competitions performed in the current swarm at each generation. Experimental results demonstrate the promising performance of the proposed algorithm in terms of both optimization quality and convergence speed [63]. Lin, et al. proposed an MOPSO with multiple search strategies (MMOPSO) to tackle complex MOPs, where a decomposition approach is exploited for transforming the MOPs. Two search strategies are used to update the velocity and position of each particle [64].

The factors that affect the IGD and HV metrics in MOPSO:

1) Changing the storage form of the non-dominated solution in the knowledge base, 2) Adjusting the flight parameters of the particle, and 3) Increasing the mutation of the particle. 4) Adjusting the population size adaptively. In order to improve the diversity and convergence of MOPSO, a MOPSO with dynamic population size is used to improve the diversity of each group, including a dynamic population strategy and an integration of an adaptive local archive, which can improve the diversity and convergence.

A. Convergence analysis of MOPSO

Theoretical and empirical analysis of the properties of evolutionary algorithms is very important to understand their searching behaviors and to develop more efficient algorithms. Fang, et al. proposed a quantum-behaved particle swarm optimization (QPSO) algorithm and discussed the convergence of QPSO within the framework of random algorithms’ global convergence theorem [65]. In [66], Tian, et al. presented the convergence analysis with construction coefficient, limit, differential equation, Z transformation, and matrix. Meanwhile, if the condition in eq.(14) is met, the position of a single particle will tend to be (φ1pi+φ2pg)/(φ1+φ2).

$\{\begin{array}{l}1-\omega \ge 0\\ 2\omega +2\ge {\phi }_1+{\phi }_2\end{array},$ (14)

The convergence analysis of MOPSO contains the theory of probability principle and Lyapunov stability theorem.

In [67], Sun, et al. investigated in detail the convergence of the MOPSO algorithm on a probabilistic metric space and proved that the MOPSO algorithm is a form of contraction mapping and can converge to the global optimum. This is the first time that the theory of probabilistic metric spaces has been employed to analyze a stochastic optimization algorithm.

Then, Kadirkamanathan, et al. [68] proved a more generalized stability analysis of the particle dynamics using the Lyapunov stability theorem. Moreover, Van, et al. proved that particles could converge to a stable point [69]. In [70], the swarm state sequence is defined and its Markov properties are examined according to the theory of MOPSO. Two closed sets, the optimal particle state set and optimal swarm state set, are then obtained. In the previous work, several variants of the MOPSO algorithm have been proposed to handle the MOPs based on the concept and the Pareto optimality. However, a fairly small number of scholars have analyzed and proved the convergence of their improved MOPSO algorithms. In [71], Chakraborty, et al. presented the first, simple analysis of the general Pareto-based MOPSO and found conditions on its most important control parameters (the inertia factor and acceleration coefficients) that govern the convergence behavior of the algorithm to the optimal Pareto front in the objective function space.

In [72], Li, et al. presented a novel MOPSO algorithm based on the global margin ranking (GMR) strategy, which deploys the position information of individuals in objective space to gain the margin of dominance throughout the population. In order to ensure the convergence of the proposed MOPSO algorithm, it gives a convergence analysis and ranking efficiency analysis to verify the effectiveness.

MOPSO has been accepted widely as a potential global optimization algorithm, but there is still great space for the research of the algorithm itself [73]. So far, the mathematical proofs of convergence, convergent velocity, parameter selection, and robustness have not been proposed perfectly on MOPSO. Hence, how to study and analyze MOPSO by the ideas of limit, probability, evolution, and topology to reflect the mechanism of how MOPSO works, which is also a highly desired subject that should be paid much attention to by MOPSO researchers.

B. Timing complexity of MOPSO

The time complexity analysis of MOPSO is a significant issue to apply to different fields. The commonly used computation methods of time complexity can be summed up as the summation and recursion method. In [37], Moubayed, et al. presented that the time complexity was calculated by the proposed D2MOPSO, that the global set N and the population size K. Since K is equal to N, it follows from this analysis that D²MOPSO has similar computational complexity to the other comparable algorithms. D²MOPSO uses the e archive (of size L ≤ N), which is updated on each iteration. In order to select the global leader for each particle, all solutions in the external archive are checked for the best aggregation value. The complexity would then be O(2LN) ~ O(N). When an external archive (of size K > N) is used, the complexity becomes O(KN + 2LN) ~ O(KN).

In [20], Coello, et al. investigated that the adaptive grid was lower than niching [i.e., O(N²)]. In [36], Raquel, et al. investigate the time complexity in MOPSO with the original crowding distance. If the objectives are M and population size is N, the overall complexity of MOPSO-CD will be O(MN²).

In addition, the convergence time of particle swarm optimization is analyzed on the facet of particle interaction [74], in which the theoretical analysis is conducted on the social-only model of MOPSO instead of on common models in practice. The theoretical results reveal the relationship between the convergence time and the level of convergence as well as the relationship between the convergence time and the swarm size.

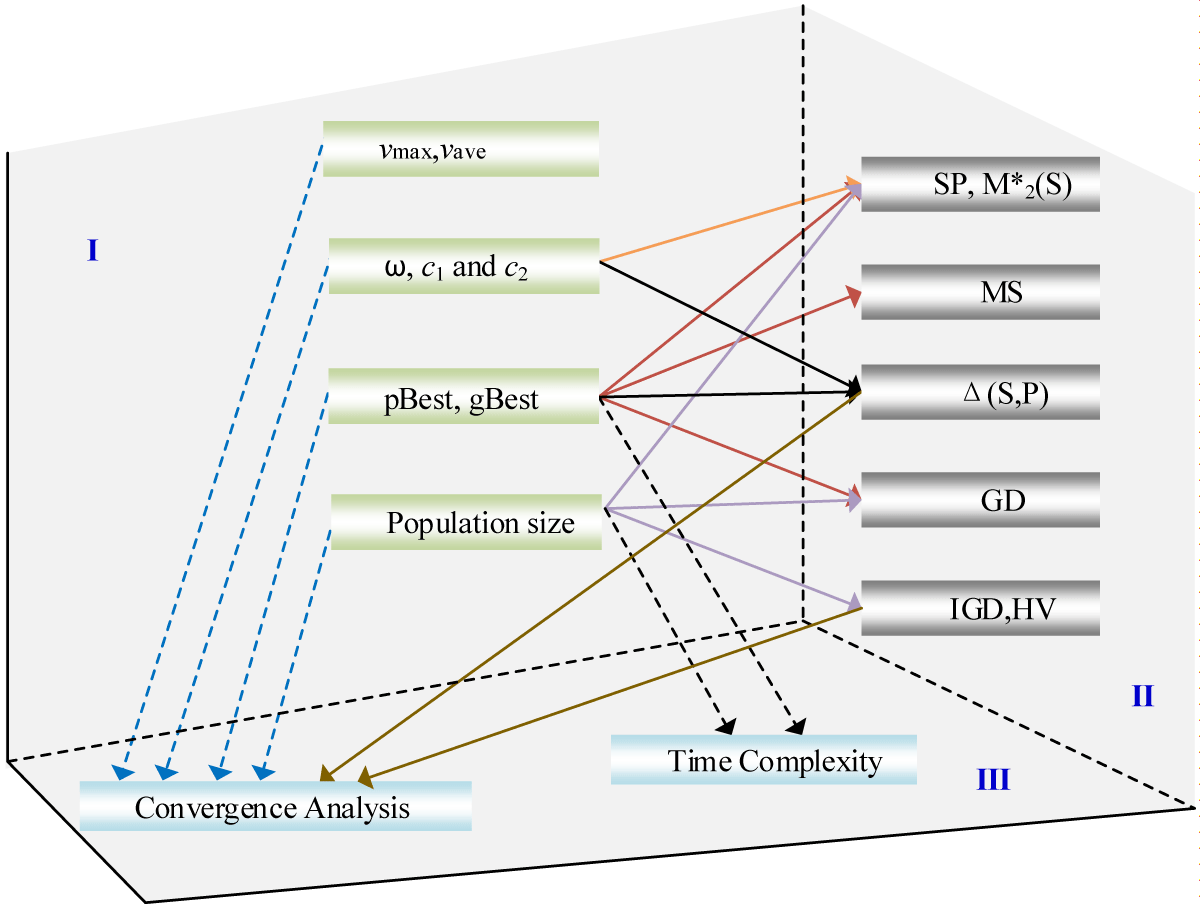
In total, the major relation of the key parameters, the performance metrics, and the theoretical analysis of MOPSO is shown in Figure 4.

Although there has been a lot of research work on the theoretical analysis, more problems often need to be considered according to the practical applications. Based on the operational principle of MOPSO, several potential future research directions in the area of MOPSO have been listed as follows.

A. The trade-off between rapidity and diversity

Rapidity is a pursuit of algorithms in solving an MOP. In the practical application, it is usually necessary to consider both rapidity and diversity at the same time. At present, many researchers have proposed several approaches to decrease the time complexity and improve the diversity of MOPSO, but it is so hard to reach the desirable objectives. In [45], a local search enhanced MOPSO is used for scheduling textile production processes, where the time complexity and diversity are considered comprehensively. As more and more practical cases in solving the MOPs are being studied, the rapidity and diversity need to be paid attention to and studied in future work.

B. Dynamic multi-objective optimization problems

One of the most major distinguishing features of dynamic multi-objective optimization problems (DMOPs) is that the objectives are time-varying. At present, the existing MOPSO algorithms cannot obtain satisfactory optimization effects when handling DMOPs. Therefore, it is urgent to study an MOPSO algorithm that can solve the dynamic multi-objective problem. In [75], Jiang, et al. presented a transfer learning mechanism and incorporated the proposed approach into the development of an MOPSO algorithm to solve the complex DMOPs. The experimental results confirm the effectiveness of the proposed design for DMOPs. Although there are many presented MOPSO algorithms, few improved MOPSO algorithms are for their characteristics of optimization process.

Most scholars verify the MOPSO algorithm through the static multi-objective optimization problem, and a few scholars have studied the application of the MOPSO algorithm in the complex dynamic process.

C. The many-objective large-scale optimization

Traditional research about MOPSO algorithm focuses on MOPs with small numbers of variables and fewer than four objectives. However, with the complexity of the big data era, more and more multi-objective optimization problems will exceed three objectives. CAO, et al. presented many-objective large-scale optimization problems (MaOLSOPs). We need to explore thoroughly parallel attributes of the particle swarm and design the novel PSO algorithms according to the characteristics of distributed parallel computation [76]. In the process of calculation, when the objective number is large and the number of variables is huge, the optimization process will be extremely time-consuming [77-81]. Therefore, it is very necessary for research to be effective in addition to large-scale multi-objective problems.

D. More theoretical guarantee

Although some scholars have conducted some theoretical research on the MOPSO algorithm, it has been shown that the MOPSO algorithm is effective for the practical multi-objective optimization problem, but a strict mathematical proof of the convergence of the MOPSO algorithm is not given. In [71], Chakraborty, et al. presented the stability and convergence properties of the MOPSO algorithm, which includes the analysis of the general Pareto-based MOPSO and finds conditions on its most important control parameters (the inertia factor and acceleration coefficients) [82]. However, the above methods need too many hypothetical prerequisites. Therefore, the theoretical proofs of the MOPSO algorithm are still a shortage, and further research needs to be conducted [83-86].

E. Stagnation of particles in the last stage

Although during the last ten years, research on and with MOPSO has reached an improvement state, there are still many open problems, and new application areas are continually emerging for the MOPSO algorithm [87-90]. Below, we unfold some important future directions of research in the area of MOPSO. Given the problem of parameter adjustment in the MOPSO algorithm, how to judge the current population evolution environment by a comprehensive evaluation index and make a unified adjustment to the parameters of the MOPSO algorithm [91].

F. Self-organization MOPSO

In the process of optimizing the MOPSO algorithm, how to realize the optimization method of the whole particle swarm optimization and find the optimal solution set closest to the real Pareto frontier are two crucial problems [92-94]. In particular, a population structure is the foundation of a swarm, and different structures may drive the swarm to behave differently. Through the analysis of particle behavior in a search process, dynamic population size strategies are used. In [95-97], an adaptive MOPSO based on clustering considers the population topology and individual behavior control together to balance local and global search in an optimization process. Meanwhile, it separates the swarm dynamically in the searching process to connect the subpopulation clusters and uses a ring neighborhood topology to share the information among these clusters. Though many approaches have been proposed, one of the important questions is whether there are other effective evaluation methods to evaluate the effectiveness of the individual particles. Therefore, the self-organization MOPSO algorithm needs to be studied in future work.

In conclusion, the MOPSO algorithm has emerged as a potent tool for handling complex multi-objective optimization problems within a competitive-cooperative framework. This review paper has provided a comprehensive survey of MOPSO, encompassing its basic principles, key parameters, advanced methods, theoretical analyses, and performance metrics. The analysis of parameters influencing convergence and diversity performance has offered insights into the searching behavior of particles in MOPSO. The discussion on advanced MOPSO methods has highlighted various strategies to enhance the algorithm’s efficiency, such as selecting proper g-Best and p-Best solutions, employing hybrid approaches with other intelligent algorithms, and adjusting population sizes dynamically. The theoretical analysis section has delved into convergence and timing complexity of MOPSO, shedding light on its mathematical foundations and practical implications.

Despite the significant progress in MOPSO research over the last two decades, several potential future research directions have been identified. These include exploring the application of MOPSO in complex dynamic processes, addressing the many-objective large-scale optimization challenges, providing more theoretical guarantees, and overcoming stagnation issues in particle evolution. In particular, there is a need for unified parameter adjustment methods, self-organization capabilities, and real-world applications of MOPSO to further solidify its position as a leading algorithm in multi-objective optimization.

Overall, this review paper has aimed to provide a comprehensive understanding of MOPSO’s developments, achievements, and future directions, fostering further research and advancements in this promising field.

1. Li H, Landa-Silva D. An adaptive evolutionary multi-objective approach based on simulated annealing. Evol Comput. 2011;19(4):561–595. Available from: https://dl.acm.org/toc/evol/2011/19/4
2. Brockhoff D, Zitzler E. Objective reduction in evolutionary multi-objective optimization: theory and applications. Evol Comput. 2009;17(2):135–166. Available from: https://ph02.tci-thaijo.org/index.php/sej/article/view/123003
3. Hu WW, Tan Y. Prototype generation using multi-objective particle swarm optimization for nearest neighbor classification. IEEE Trans Cybern. 2016;46(12):2719–2731. Available from: https://doi.org/10.1109/TCYB.2015.2487318
4. Zhang Y, Gong DW, Cheng J. Multi-objective particle swarm optimization approach for cost-based feature selection in classification. IEEE ACM Trans Comput Biol Bioinform. 2017;14(1):64–75.
5. Zhang X, Tian Y, Cheng R. An efficient approach to nondominated sorting for evolutionary multi-objective optimization. IEEE Trans Evol Comput. 2015;19(2):201–213. Available from: http://dx.doi.org/10.1109/TEVC.2014.2308305
6. Deb K, Pratap A, Agarwal S, Meyarivan T. A fast and elitist multi-objective genetic algorithm: NSGA-II. IEEE Trans Evol Comput. 2002;6(2):182–197. Available from: https://research.birmingham.ac.uk/en/publications/a-fast-and-elitist-multi-objective-genetic-algorithm-nsga-ii
7. Mathijssen G, Lefeber D, Vanderborght B. Variable recruitment of parallel elastic elements: series–parallel elastic actuators (SPEA) with dephased mutilated gears. IEEE ASME Trans Mechatron. 2015;20(2):594–602. Available from: https://researchportal.vub.be/en/publications/variable-recruitment-of-parallel-elastic-elements-series-parallel
8. Helwig S, Branke J, Mostaghim S. Experimental analysis of bound handling techniques in particle swarm optimization. IEEE Trans Evol Comput. 2013;17(2): Available from: http://dx.doi.org/10.1109/TEVC.2012.2189404
9. Zitzler E, Laumanns M, Thiele L. SPEA2: Improving the strength Pareto evolutionary algorithm. Comput Eng Netw Lab (TIK), Zurich, Switzerland. 2001;(103):259–271. Available from: https://sop.tik.ee.ethz.ch/publicationListFiles/zlt2001a.pdf
10. Ali H, Khan FA. Attributed multi-objective comprehensive learning particle swarm optimization for optimal security of networks. Appl Soft Comput. 2013;13(9):3903–3921.
11. Mathijssen G, Lefeber D, Vanderborght B. Variable recruitment of parallel elastic elements: Series–parallel elastic actuators (SPEA) with dephased mutilated gears. IEEE ASME Trans Mechatron. 2015;20(2):594–602.
12. Helwig S, Branke J, Mostaghim S. Experimental analysis of bound handling techniques in particle swarm optimization. IEEE Trans Evol Comput. 2013;17(2):259–271. Available from: https://ieeexplore.ieee.org/document/6163405
13. Pehlivanoglu YV. A new particle swarm optimization method enhanced with a periodic mutation strategy and neural networks. IEEE Trans Evol Comput. 2013;17(3):436–452. Available from: https://ieeexplore.ieee.org/document/6210488
14. He X, Zhou Y, Chen Z. An evolution path-based reproduction operator for many-objective optimization. IEEE Trans Evol Comput. 2017. Available from: https://ieeexplore.ieee.org/document/8226783
15. Han H, Lu W, Zhang L, Qiao J. Adaptive gradient multi-objective particle swarm optimization. IEEE Trans Cybern. 2017. Available from: https://ieeexplore.ieee.org/document/8063385
16. Feng L, Mao Z, Yuan P, et al. Multi-objective particle swarm optimization with preference information and its application in electric arc furnace steelmaking process. Struct Multidiscip Optim. 2015;52(5):1013–1022. Available from: https://link.springer.com/article/10.1007/s00158-015-1276-2
17. Bonabeau E, Dorigo M, Theraulaz G. Swarm Intelligence: From Natural to Artificial Systems. New York (NY): Oxford University Press; 1999. Available from: https://academic.oup.com/book/40811
18. Li K, Deb K, Zhang Q, Kwong S. An evolutionary many-objective optimization algorithm based on dominance and decomposition. IEEE Trans Evol Comput. 2015;19(5):694–716. Available from: https://ieeexplore.ieee.org/document/6964796
19. Mukhopadhyay A, Maulik U, Bandyopadhyay S, Coello CAC. A survey of multi-objective evolutionary algorithms for data mining: Part I. IEEE Trans Evol Comput. 2014;18(1):4–19. Available from: https://ieeexplore.ieee.org/document/6658835
20. Coello CAC, Pulido GT, Lechuga MS. Handling multiple objectives with particle swarm optimization. IEEE Trans Evol Comput. 2004;8(3):256–279. Available from: https://ieeexplore.ieee.org/document/1304847
21. Ganguly S, Sahoo NC, Das D. Multi-objective particle swarm optimization based on fuzzy-Pareto-dominance for possibilistic planning of electrical distribution systems incorporating distributed generation. Fuzzy Sets Syst. 2013;213:47–73. Available from: https://doi.org/10.1016/j.fss.2012.07.005
22. Chang WD, Chen CY. PID controller design for MIMO processes using improved particle swarm optimization. Circ Syst Signal Process. 2014;33(5):1473–1490. Available from: https://link.springer.com/article/10.1007/s00034-013-9710-4
23. Mahmoodabadi MJ, Taherkhorsandi M, Bagheri A. Optimal robust sliding mode tracking control of a biped robot based on ingenious multi-objective PSO. Neurocomputing. 2014;124:194–209. Available from: https://doi.org/10.1016/j.neucom.2013.07.009
24. Chen GG, Liu L, Song P, Du Y. Chaotic improved PSO based multi-objective optimization for minimization of power losses and L index in power systems. Energy Convers Manag. 2014;86:548–560. Available from: https://doi.org/10.1016/j.enconman.2014.06.003
25. Liu J, Luo XG, Zhang XMF. Job scheduling algorithm for cloud computing based on particle swarm optimization. Adv Mater Res. 2013;662:957–960. Available from: https://www.scientific.net/AMR.662.957
26. Chou CJ, Lee CY, Chen CC. Survey of reservoir grounding system defects considering the performance of lightning protection and improved design based on soil drilling data and the particle swarm optimization technique. IEEE Trans Electr Electron Eng. 2014;9(6):605–613. Available from: https://doi.org/10.1002/tee.22016
27. Xu YJ, You T. Minimizing thermal residual stresses in ceramic matrix composites by using iterative Map Reduce guided particle swarm optimization algorithm. Compos Struct. 2013;99:388–396. Available from: https://doi.org/10.1016/j.compstruct.2012.11.027
28. Clerc M, Kennedy J. The particle swarm—explosion, stability, and convergence in a multidimensional complex space. IEEE Trans Evol Comput. 2002;6(1):58–73. Available from: https://ieeexplore.ieee.org/document/985692
29. Reyes-Sierra M, Coello CAC. Multi-objective particle swarm optimizers: A survey of the state-of-the-art. Int J Comput Intell Res. 2006;2(3):287–308. Available from: https://www.researchgate.net/publication/216301306
30. Peng G, Fang YW, Peng WS, Chai D, Xu Y, et al. Multi-objective particle optimization algorithm based on sharing–learning and dynamic crowding distance. Optik. 2016;127(12):5013–5020. Available from: http://dx.doi.org/10.1109/ChiCC.2016.7554815
31. Ayachitra A, Vinodha R. Comparative study and implementation of multi-objective PSO algorithm using different inertia weight techniques for optimal control of a CSTR process. ARPN J Eng Appl Sci. 2015;10(22):10395–10404.
32. Jordehi AR. Particle swarm optimisation (PSO) for allocation of FACTS devices in electric transmission systems: A review. Renew Sustain Energy Rev. 2015;52:1260–1267. Available from: https://doi.org/10.1016/j.rser.2015.08.007
33. Hu W, Yen GG. Adaptive multi-objective particle swarm optimization based on parallel cell coordinate system. IEEE Trans Evol Comput. 2015;19(1):1–18. Available from: https://ieeexplore.ieee.org/document/6692894
34. Leong WF, Yen GG. PSO-based multi-objective optimization with dynamic population size and adaptive local archives. IEEE Trans Syst Man Cybern B Cybern. 2008;38(5):1270–1293. Available from: https://ieeexplore.ieee.org/document/4581390
35. Meza J, Espitia H, Montenegro C, Giménez E, González-Crespo R. MOVPSO: Vortex multi-objective particle swarm optimization. Appl Soft Comput. 2017;52:1042–1057. Available from: https://doi.org/10.1016/j.asoc.2016.09.026
36. Raquel CR, Nava PC. An effective use of crowding distance in multi-objective particle swarm optimization. In: Proc. Genetic Evol Comput. 2005:257–264. Available from: https://www.researchgate.net/publication/220741476
37. Al Moubayed N, Petrovski A, McCall J. D2MOPSO: MOPSO based on decomposition and dominance with archiving using crowding distance in objective and solution spaces. Evol Comput. 2014;22(1):47–77. Available from: https://ieeexplore.ieee.org/document/6818671
38. Agrawal S, Panigrahi BK, Tiwari MK. Multi-objective particle swarm algorithm with fuzzy clustering for electrical power dispatch. IEEE Trans Evol Comput. 2008;12(5):529–541. Available from: https://ieeexplore.ieee.org/document/4454712
39. Andervazh MR, Olamaei J, Haghifam MR. Adaptive multi-objective distribution network reconfiguration using multi-objective discrete particle swarm optimisation algorithm and graph theory. IET Gener Transm Distrib. 2013;7(12):1367–1382. Available from: https://doi.org/10.1049/iet-gtd.2012.0712
40. Daneshyari M, Yen GG. Cultural-based multi-objective particle swarm optimization. IEEE Trans Syst Man Cybern B Cybern. 2011;41(2):553–567. Available from: https://ieeexplore.ieee.org/document/5567177
41. Ali H, Khan FA. Attributed multi-objective comprehensive learning particle swarm optimization for optimal security of networks. Appl Soft Comput. 2013;13(9):3903–3921. Available from: https://www.sciencedirect.com/science/article/abs/pii/S1568494613001397
42. Lee KB, Kim JH. Multi-objective particle swarm optimization with preference-based sort and its application to path following footstep optimization for humanoid robots. IEEE Trans Evol Comput. 2013;17(6):755–766. Available from: https://ieeexplore.ieee.org/document/6414622
43. Zheng YJ, Ling HF, Xue JY, Chen SY. Population classification in fire evacuation: A multi-objective particle swarm optimization approach. IEEE Trans Evol Comput. 2014;18(1). Available from: https://ieeexplore.ieee.org/document/6595531
44. Torabi SA, Sahebjamnia N, Mansouri SA, Bajestani MA. A particle swarm optimization for a fuzzy multi-objective unrelated parallel machines scheduling problem. Appl Soft Comput. 2013;13(12):4750–4762. Available from: https://doi.org/10.1016/j.asoc.2013.07.029
45. Zhang R, Chang PC, Song S, Wu C. Local search enhanced multi-objective PSO algorithm for scheduling textile production processes with environmental considerations. Appl Soft Comput. 2017;61:447–467. Available from: https://doi.org/10.1016/j.asoc.2017.08.013
46. Shim VA, Tan KC, Chia JY. Multi-objective optimization with estimation of distribution algorithm in a noisy environment. Evol Comput. 2013;21(1):149–177. Available from: https://doi.org/10.1162/evco_a_00066
47. Yue C, Qu B, Liang J. A multi-objective particle swarm optimizer using ring topology for solving multimodal multi-objective problems. IEEE Trans Evol Comput. 2017. Available from: https://ieeexplore.ieee.org/document/8046023
48. Huang VL, Suganthan PN, Liang JJ. Comprehensive learning particle swarm optimizer for solving multi-objective optimization problems. Int J Intell Syst. 2006;21(2):209–226. Available from: http://dx.doi.org/10.1002/int.20128
49. Tsai SJ, Sun TY, Liu CC, Hsieh ST, Wu WC, Chiu SY. An improved multi-objective particle swarm optimizer for multi-objective problems. Expert Syst Appl. 2010;37(8):5872–5886. Available from: https://doi.org/10.1016/j.eswa.2010.02.018
50. Cheng S, Zhan H, Shu Z. An innovative hybrid multi-objective particle swarm optimization with or without constraints handling. Appl Soft Comput. 2016;47:370–388. Available from: https://doi.org/10.1016/j.asoc.2016.06.012
51. Ali H, Khan FA. Attributed multi-objective comprehensive learning particle swarm optimization for optimal security of networks. Appl Soft Comput. 2013;13(9):3903–3921. Available from: https://doi.org/10.1016/j.asoc.2013.04.015
52. Tang B, Zhu Z, Shin HS, Tsourdos A, Luo J. A framework for multi-objective optimisation based on a new self-adaptive particle swarm optimisation algorithm. Inf Sci. 2017;420:364–385. Available from: https://doi.org/10.1016/j.ins.2017.08.076
53. Zhu Q, Lin Q, Chen W, Wong KC, Coello CA, Li J. An external archive-guided multi-objective particle swarm optimization algorithm. IEEE Trans Cybern. 2017;47(9):2794–2808. Available from: https://ieeexplore.ieee.org/document/7946155
54. Wang Y, Yang Y. Particle swarm optimization with preference order ranking for multi-objective optimization. Inf Sci. 2009;179(12):1944–1959. Available from: https://doi.org/10.1016/j.ins.2009.01.005
55. Alvarez-Benítez JE, Everson RM, Fieldsend JE. A MOPSO algorithm based exclusively on Pareto dominance concepts. In: Evol Multi-Criterion Optimiz. 2005:459–473. Available from: https://link.springer.com/chapter/10.1007/978-3-540-31880-4_32
56. Wang Y, Yang Y. Particle swarm with equilibrium strategy of selection for multi-objective optimization. Eur J Oper Res. 2010;200(1):187–197. Available from: https://doi.org/10.1016/j.ejor.2008.12.026
57. Yen GG, Leong WF. Dynamic multiple swarms in multi-objective particle swarm optimization. IEEE Trans Syst Man Cybern A Syst Hum. 2009;39(4):890–911. Available from: https://ieeexplore.ieee.org/document/4783028
58. Goh CK, Tan KC, Liu DS, Chiam SC. A competitive and cooperative co-evolutionary approach to multi-objective particle swarm optimization algorithm design. Eur J Oper Res. 2010;202(1):42–54. Available from: https://doi.org/10.1016/j.ejor.2009.05.005
59. Cheng S, Zhao L, Jiang X. An effective application of bacteria quorum sensing and circular elimination in MOPSO. IEEE/ACM Trans Comput Biol Bioinform. 2017;14(1):56. Available from: https://ieeexplore.ieee.org/document/7128359
60. De Carvalho AB, Pozo A. Measuring the convergence and diversity of CDAS multi-objective particle swarm optimization algorithms: a study of many-objective problems. Neurocomputing. 2012;75(1):43-51. Available from: https://doi.org/10.1016/j.neucom.2011.03.053
61. Wang H, Fu Y, Huang M, Wang J. A hybrid evolutionary algorithm with adaptive multi-population strategy for multi-objective optimization problems. Soft Comput. 2016:1-13. Available from: https://link.springer.com/article/10.1007/s00500-016-2414-5
62. Britto A, Pozo A. Using reference points to update the archive of MOPSO algorithms in many-objective optimization. Neurocomputing. 2014;127:78-87. Available from: https://doi.org/10.1016/j.neucom.2013.05.049
63. Zhang X, Zheng X, Cheng R, Qiu J, Jin Y. A competitive mechanism-based multi-objective particle swarm optimizer with fast convergence. Inf Sci. 2018;427:63-76. Available from: https://doi.org/10.1016/j.ins.2017.10.037
64. Lin Q, Li J, Du Z, Chen J, Ming Z. A novel multi-objective particle swarm optimization with multiple search strategies. Eur J Oper Res. 2015;247(3):732-744. Available from: https://doi.org/10.1016/j.ejor.2015.06.071
65. Fang W, Sun J, Xie Z, Xu W. Convergence analysis of quantum-behaved particle swarm optimization algorithm and study on its control parameter. Acta Phys Sin. 2010;59(6):3686-3694. Available from: https://doi.org/10.7498/aps.59.3686
66. Tian DP. A review of convergence analysis of particle swarm optimization. Int J Grid Distrib Comput. 2013;6(6):117-128. Available from: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=ed4cdddfc04dfe9eb101af85faa1dcc251790b8b
67. Sun J, Wu X, Palade V, Fang W, Lai CH, Xu W. Convergence analysis and improvements of quantum-behaved particle swarm optimization. Inf Sci. 2012;193(15):81-103. Available from: https://citeseerx.ist.psu.edu/document?repid=rep1&type=pdf&doi=71a72d2155a2443279f73a9dd71732762b2e400e
68. Kadirkamanathan V, Selvarajah K, Fleming PJ. Stability analysis of the particle dynamics in particle swarm optimizer. IEEE Trans Evol Comput. 2006;10(3):245-255. Available from: https://doi.org/10.1109/TEVC.2005.857077
69. Van den Bergh F, Engelbrecht AP. A study of particle swarm optimization particle trajectories. Inf Sci. 2006;176(8):937-971. Available from: https://doi.org/10.1016/j.ins.2005.02.003
70. Xu G, Yu G. Reprint of: On convergence analysis of particle swarm optimization algorithm. J Comput Appl Math. 2018;340:709–17. Available from: https://doi.org/10.1016/j.cam.2018.04.036
71. Chakraborty P, Das S, Roy GG, Abraham A. On convergence of the multi-objective particle swarm optimizers. Inf Sci. 2011;181(8):1411–25. Available from: https://doi.org/10.1016/j.ins.2010.11.036
72. Li L, Wang W, Xu X. Multi-objective Particle Swarm Optimization based on Global Margin Ranking. Inf Sci. 2016;375:30–47. Available from: https://doi.org/10.1016/j.ins.2016.08.043
73. Han H, Lu W, Zhang L, Qiao J. Adaptive Gradient Multiobjective Particle Swarm Optimization. IEEE Trans Cybern. 2018;48(11):3067–79. Available from: https://doi.org/10.1109/tcyb.2017.2756874
74. Chen CH, Chen YP. Convergence Time Analysis of Particle Swarm Optimization Based on Particle Interaction. Adv Artif Intell. 2011;2011(1):1–7. Available from: https://doi.org/10.1155/2011/204750
75. Jiang M, Huang Z, Qiu L, Huang WZ, Yen GG. Transfer Learning based Dynamic Multi-objective Optimization Algorithms. IEEE Trans Evol Comput. 2018;22:501–4. Available from: https://doi.org/10.1109/TEVC.2017.2771451
76. Cao B, Zhao J, Lv Z, Liu X, Yang S, Kang X, et al. Distributed Parallel Particle Swarm Optimization for Multi-Objective and Many-Objective Large-Scale Optimization. IEEE Access. 2017;5(99):8214–21. Available from: https://doi.org/10.1109/ACCESS.2017.2702561
77. Yang Y, Zhang T, Yi W, Yi W, Kong L, Li X, et al. Deployment of multistatic radar system using multi-objective particle swarm optimization. IET Radar Sonar Navig. 2018;12(5):485–93. Available from: https://doi.org/10.1049/iet-rsn.2017.0351
78. Fernández-Rodríguez A, Fernández-Cardador A, Cucala AP, Domínguez M. Design of Robust and Energy-Efficient ATO Speed Profiles of Metropolitan Lines Considering Train Load Variations and Delays. IEEE Trans Intell Transp Syst. 2015;16(4):2061–71. Available from: https://doi.org/10.1109/TITS.2015.2391831
79. Wen S, Lan H, Fu Q, Zhang L. Economic Allocation for Energy Storage System Considering Wind Power Distribution. IEEE Trans Power Syst. 2015;30(2):644–52. Available from: https://doi.org/10.1109/TPWRS.2014.2337936
80. Shahsavari A, Mazhari SM, Fereidunian A. Fault Indicator Deployment in Distribution Systems Considering Available Control and Protection Devices: A Multi-Objective Formulation Approach. IEEE Trans Power Syst. 2014;29(5):2359–69. Available from: https://doi.org/10.1109/TPWRS.2014.2303933
81. Srivastava L, Singh H. Hybrid multi-swarm particle swarm optimisation based multi-objective reactive power dispatch. IET Gener Transm Distrib. 2015;9(8):727–39. Available from: https://doi.org/10.1049/iet-gtd.2014.0469
82. Niknam T, Narimani MR, Aghaei J. Improved particle swarm optimisation for multi-objective optimal power flow considering the cost, loss, emission and voltage stability index. IET Gener Transm Distrib. 2012;6(6):515–27. Available from: https://doi.org/10.1049/iet-gtd.2011.0851
83. Chamaani S, Mirtaheri SA, Abrishamian MS. Improvement of Time and Frequency Domain Performance of Antipodal Vivaldi Antenna Using Multi-Objective Particle Swarm Optimization. IEEE Trans Antennas Propag. 2011;59(5):1738–42. Available from: https://doi.org/10.1109/TAP.2011.2122290
84. Karimi E, Ebrahimi A. Inclusion of Blackouts Risk in Probabilistic Transmission Expansion Planning by a Multi-Objective Framework. IEEE Trans Power Syst. 2015;30(5):2810–7. Available from: https://doi.org/10.1109/TPWRS.2014.2370065
85. Ho SL, Yang J, Yang S, Bai Y. Integration of Directed Searches in Particle Swarm Optimization for Multi-Objective Optimization. IEEE Trans Magn. 2015;51(3):1–4. Available from: http://dx.doi.org/10.1109/TMAG.2014.2361323
86. Pham MT, Zhang D, Chang SK. Multi-Guider and Cross-Searching Approach in Multi-Objective Particle Swarm Optimization for Electromagnetic Problems. IEEE Trans Magn. 2012;48(2):539–42. Available from: https://doi.org/10.1109/TMAG.2011.2173559
87. Ye X, Chen H, Liang H, Xinjun C, Jiaxin Y. Multi-Objective Optimization Design for Electromagnetic Devices With Permanent Magnet Based on Approximation Model and Distributed Cooperative Particle Swarm Optimization Algorithm. IEEE Trans Magn. 2017;PP(99):1–5. Available from: https://doi.org/10.1109/TMAG.2017.2758818
88. Ganguly S. Multi-Objective Planning for Reactive Power Compensation of Radial Distribution Networks With Unified Power Quality Conditioner Allocation Using Particle Swarm Optimization. IEEE Trans Power Syst. 2014;29(4):1801–10. Available from: https://doi.org/10.1109/TPWRS.2013.2296938
89. Shukla A, Singh SN. Multi-objective unit commitment using search space-based crazy particle swarm optimisation and normal boundary intersection technique. IET Gener Transm Distrib. 2016;10(5):1222–31. Available from: https://doi.org/10.1049/iet-gtd.2015.0806
90. Goudos SK, Zaharis ZD, Kampitaki DG, Rekanos IT, Hilas CS. Pareto Optimal Design of Dual-Band Base Station Antenna Arrays Using Multi-Objective Particle Swarm Optimization With Fitness Sharing. IEEE Trans Magn. 2009;45(3):1522–5. Available from: https://doi.org/10.1109/TMAG.2009.2012695
91. Xue B, Zhang M, Browne WN. Particle swarm optimization for feature selection in classification: a multi-objective approach. IEEE Trans Cybern. 2013;43(6):1656–71. Available from: https://doi.org/10.1109/TSMCB.2012.2227469
92. Eladany MM, Eldesouky AA, Sallam AA. Power System Transient Stability: An Algorithm for Assessment and Enhancement Based on Catastrophe Theory and FACTS Devices. IEEE Access. 2019;PP(99):1–1. Available from: http://dx.doi.org/10.1109/ACCESS.2019.2927680
93. Cao Y, Zhang Y, Zhang H. Probabilistic Optimal PV Capacity Planning for Wind Farm Expansion Based on NASA Data. IEEE Trans Sustain Energy. 2017;8(3):1291–300. Available from: http://dx.doi.org/10.1109/TSTE.2017.2677466
94. Ahmadi K, Salari E. Small dim object tracking using a multi-objective particle swarm optimisation technique. IET Image Process. 2015;9(9):820–6. Available from: http://dx.doi.org/10.1049/iet-ipr.2014.0927
95. Liang X, Li W, Zhang Y. An adaptive particle swarm optimization method based on clustering. Soft Comput. 2015;19(2):431–48. Available from: https://doi.org/10.1007/s00500-014-1262-4
96. Tripathi PK, Bandyopadhyay S, Pal SK. Multi-objective particle swarm optimization with time variant inertia and acceleration coefficients. Inf Sci. 2007;177(22):5033–49. Available from: https://doi.org/10.1016/j.ins.2007.06.018
97. Salazar-Lechuga M, Rowe J. Particle swarm optimization and fitness sharing to solve multi-objective optimization problems. In: Proc IEEE Evol Comput. 2005 Sep;1204–11. Available from: https://doi.org/10.1109/CEC.2005.1554827